If you have a triangle with vertices A, B, and C, how would you generate random points inside the triangle ABC?
Barycentric coordinates
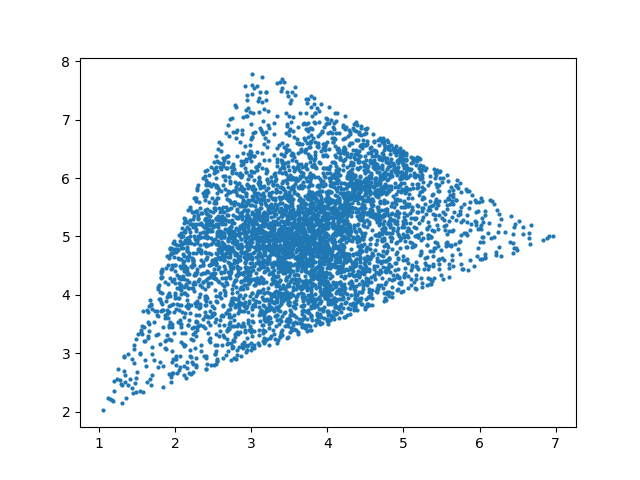
One idea would be to use barycentric coordinates.
- Generate random numbers α, β, and γ from the interval [0, 1].
- Normalize the points to have sum 1 by dividing each by their sum.
- Return αA + βB + γC.
This generates points inside the triangle, but not uniformly.
Accept-reject
Another idea is to use an accept-reject method. Draw a rectangle around the triangle, generate points in the square, and throw them away if they land outside the triangle.
An advantage to this method is that it obviously works because it doesn’t rely on anything subtle. Three cheers for brute force!
The method is fairly efficient; on average only half the points will be rejected.
A disadvantage to all accept-reject methods is that they have variable runtime, though this only matters in some applications.
Accept-flip
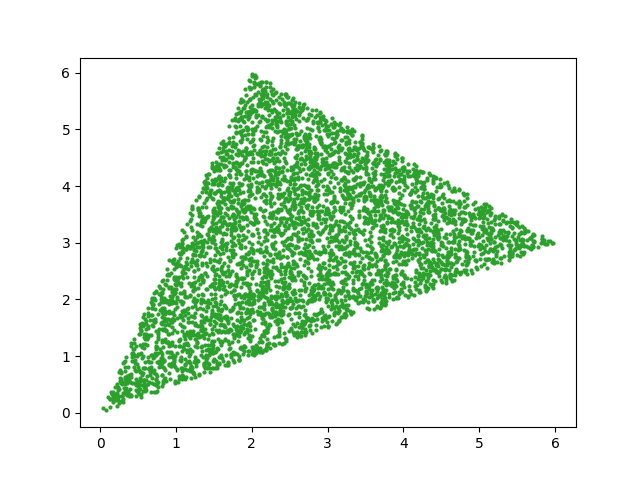
There is a clever variation on the accept-reject method. Create a parallelogram by attaching a flipped copy of the triangle. Now randomly sample from the parallelogram. Every sample point will either land inside the original triangle or in its flipped twin. If it landed in the original triangle, keep it. If it landed in the twin, flip it back over and use that point.
This is like an accept-reject method, except there’s no waste. Every point is kept, possibly after flipping.
You can find code for implementing this method on Stack Overflow.
Barycentric coordinates fixed
Felix left a note in the comments that the barycentric approach would work if you draw the random weights from an exponential distribution rather than a uniform distribution. That goes against my intuition. I thought about using a different distribution on the weights, but I didn’t work out what it would need to be, but I did not expect it to be exponential. Apparently it works. Here’s a proof by plot:
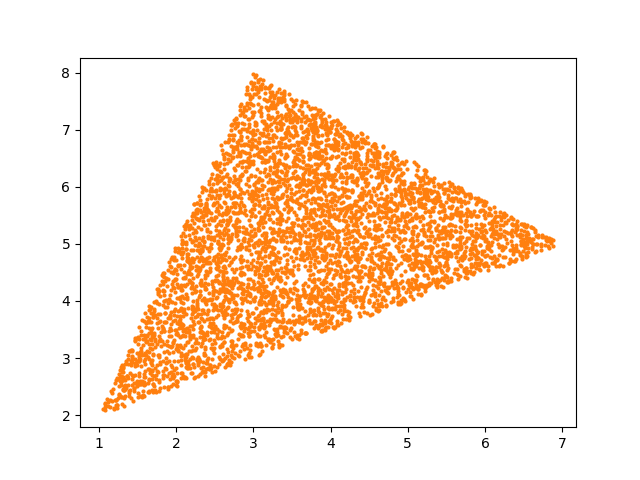

Worth noting that your Method 1 actually works when the 3 random variables follow an exponential distribution (scale doesn’t matter, but should be the same for all three).
Another fun method that also generalizes to higher-dimensional simplexes is to generate N-1 independent uniform random variables in [0, 1], sort them from smallest to largest, and take successive differences (including boundaries 0 and 1). For instance if a <= b, then the weights become: (a – 0), (b – a), (1 – b). These already sum to 1 by construction, and can be used as barycenter coordinates.
Why not remap the parallelogram to a rectangle to have a zero waste ? Or consider 4 identical parallelograms side by side, so that their centers form a rectangle easy to cover with a uniform distribution and then use a few modulos to remap to the original triangle ?
I like this.
You ever tried to find the deepest point in an arbitrary (concave, convex, etc) polygon?
I ended up using deepest (furthest interior point from edge) of N random points in bounding box. Then deepest of N random points inside DEPTH radius circle centered at that point. Then a circle half that radius. Then half again. And so on 2 or 3 times.
Which is pretty brute but it’s the best I’ve found.
You got a better way?
@ Philippe There’s no waste in the method given in the post.
@ John,
For sampling from a polygon, reduce it to the union of simplexes (n-dimensional equivalent of triangulation). Then pick a simplex according to the volume of each and sample uniformly from that simplex using the standard algorithm.
Doing the triangulation may be complex, depending on your representation.
@Ted I like that idea. It’s simple enough that it’s obviously correct.
Barycentric one seems to work for me if I sample two numbers randomly and third number is (1-sum of other two sampled numbers). Third number can be negative sometime so I discard those cases. Visually I am getting uniform distribution of points in the triangle.
Just out of curiosity, I asked this question (in Italian, because I am lazy) to Claude. It came out with the three methods, which I suppose are common lore (it could not have been trained with this post…) but it says that barycentric coordinates are the most elegant and efficient method… See (and eventually translate)
https://claude.ai/chat/1d387ccd-445e-4450-a110-7fb5944b5634
I agree that the barycentric approach is the most elegant. Easiest to program. But you have to use the exponential distribution, not uniform.