Linear congruence random number generators have the form
xn+1 = a xn + b mod p
Inverse congruence generators have the form
xn+1 = a xn-1 + b mod p
were x-1 means the modular inverse of x, i.e. the value y such that xy = 1 mod p. It is possible that x = 0 and so it doesn’t have an inverse. In that case the generator returns b.
Linear congruence generators are quite common. Inverse congruence generators are much less common.
Inverse congruence generators were first proposed by J. Eichenauer and J. Lehn in 1986. (The authors call them inversive congruential generators; I find “inverse congruence” easier to say than “inversive congruential.”)
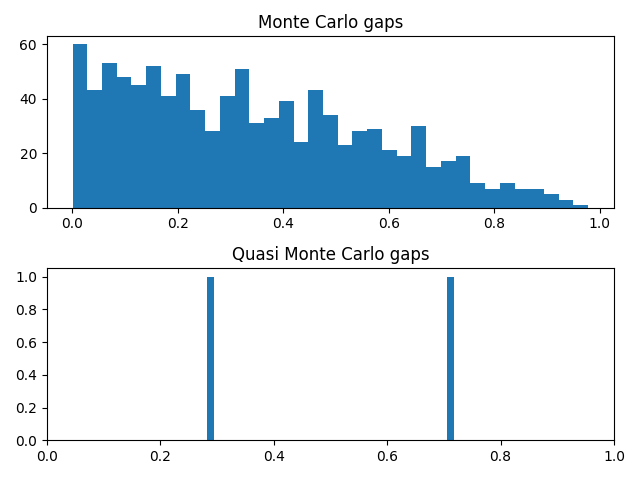
An advantage of such generators is that they have none of the lattice structure that can be troublesome for linear congruence generators. This could be useful, for example, in high-dimensional Monte Carlo integration.
These generators are slow, especially in Python. They could be implemented more efficiently in C, and would be fast enough for applications like Monte Carlo integration where random number generation isn’t typically the bottleneck.
The parameters a, b, and p have to satisfy certain algebraic properties. The parameters I’ll use in the post were taken from [1]. With these parameters the generator has maximal period p.
The generator naturally returns integers between 0 and p. If that’s what you want, then the state and the random output are the same.
If you want to generate uniformly distributed real numbers, replace x above with the RNG state, and let x be the state divided by p. Since p has 63 bits and a floating point number has 53 significant bits, all the bits of the result should be good.
Here’s a Python implementation for uniform floating point values. We pass in x and the state each time to avoid global variables.
from sympy import mod_inverse
p = 2**63 - 25
a = 5520335699031059059
b = 2752743153957480735
def icg(pair):
x, state = pair
if state == 0:
return (b/p, b)
else:
state = (a*mod_inverse(state, p) + b)%p
return (state/p, state)
If you’re running Python 3.8 or later, you can replace
mod_inverse(state, p)
with
pow(state, -1, p)
and not import sympy.
Here’s an example of calling icg to print 10 floating point values.
x, state = 1, 1
for _ in range(10):
(x, state) = icg((x, state))
print(x)
If we want to generate random bits rather than floating point numbers, we have to work a little harder. If we just take the top 32 bits, our results will be slightly biased since our output is uniformly distributed between 0 and p, not between 0 and a power of 2. This might not be a problem, depending on the application, since p is so near a power of 2.
To prevent this bias, I used a acceptance-rejection sampling method, trying again when the method generates a value above the largest multiple of 232 less than p. The code should nearly always accept.
T = 2**32
m = p - p%T
def icg32(pair):
x, state = pair
if state == 0:
return (b % T, b)
state = (a*mod_inverse(state, p) + b)%p
while state > m: # rare
state = (a*mod_inverse(state, p) + b)%p
return (state % T, state)
You could replace the last line above with
return state >> (63-32)
which should be more efficient.
The generator passes the four most commonly used test suites
- DIEHARDER
- NIST STS
- PractRand
- TestU01
whether you reduce the state mod 32 or take the top 32 bits of the state. I ran the “small crush” battery of the TestU01 test suite and all tests passed. I didn’t take the time to run the larger “crush” and “big crush” batteries because they require two and three orders of magnitude longer.
More on random number generation
[1] Jürgen Eichenauer-Herrmann. Inversive Congruential Pseudorandom Numbers: A Tutorial. International Statistical Review, Vol. 60, No. 2, pp. 167–176.