Gamma and related functions in SciPy

This page explains the following SciPy functions for computing the gamma function and related functions.

  • gamma
  • gammaln
  • gammainc
  • gamaincinv
  • gammaincc
  • gammainccinv
  • beta
  • betaln
  • betainc
  • betaincinv
  • psi
  • polygamma

The SciPy function names correspond easily to mathematical functions. However, as noted below, there are a couple things to be aware of.

  1. The functions with named ending in ln do indeed take natural logarithms, but they take absolute values first.
  2. The functions containing inc compute regularized incomplete functions and not simply incomplete functions.

These points will be made clear below.

Gamma and beta functions

The SciPy functions for gamma function Γ(z) and the beta function B(x, y) are unsurprisingly called gamma and beta. The function gamma(z) computes

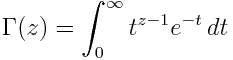
\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt

and the function beta(x, y) computes

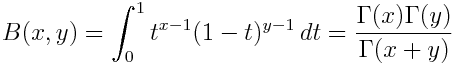
B(x,y) = \int_0^1 t^{x-1} (1-t)^{y-1} \, dt = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}

Logarithms

Often the gamma and beta functions are not as useful in practice as their logarithms. (See explanation here.) These are implemented in SciPy as gammaln and betaln. Note that gammaln actually returns the natural logarithm of the absolute value of the gamma function, i.e. gammaln(z) computes log| γ(z) |. Similarly betaln(x, y) computes log | B(x, y) |.

Psi and polygamma functions

The derivative of log( Γ(z) ) is denoted ψ(z) and is implemented in the psi function. The nth derivative of ψ(z) is implemented in psi(n, z).

Incomplete and complementary functions

Both the gamma and the beta function have “incomplete” versions. However, SciPy’s incomplete gamma function gammainc corresponds to the regularized gamma function. Similarly, SciPy’s incomplete beta function betainc corresponds to the regularized beta function.

The (lower) incomplete gamma function is defined by

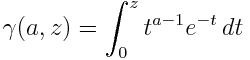
\gamma(a, z) = \int_0^z t^{a-1} e^{-t}\, dt

and the upper incomplete gamma function is defined by

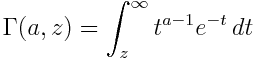
\Gamma(a, z) = \int_z^\infty t^{a-1} e^{-t}\, dt

These are called “incomplete” because they integrate over part of the region defining the gamma function. We will see below that the incomplete beta function follows the same pattern.

The regularized versions of the upper and lower incomplete gamma functions are

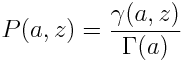
P(a, z) = \frac{\gamma(a, z)}{\Gamma(a)}

and

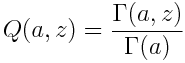
Q(a, z) = \frac{\Gamma(a, z)}{\Gamma(a)}

respectively.

The SciPy function gammainc(a, z) computes P(a, z) and the function gammaincc computes Q(a, z). Note the extra ‘c’ in gammaincc that stands for “complement.” It may not seem necessary to provide functions for both P(a, z) and its complement Q(a, z) since Q(a, z) = 1 − P(a, z). However, the complementary functions may be necessary for numerical precision. See the explanation here regarding the error function and its complement; the same reasoning applies to incomplete gamma functions.

The incomplete beta function is defined by

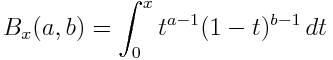
B_x(a, b) = \int_0^x t^{a-1} (1-t)^{b-1}\, dt

and the regularized incomplete beta function is defined by

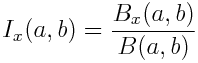
I_x(a, b) = \frac{B_x(a, b)}{B(a, b)}

The SciPy function betainc(a, b, x) computes Ix(a, b).

Inverse functions

SciPy functions ending in inv compute the inverse of the corresponding function. gammaincinv(a, y) returns x such that gammainc(a, x) equals y. Similarly gammainccinv is the inverse of gammaincc. Finally, betaincinv(a, b, y) returns x such that betaincinv(a, b, x) equals y.

There is an asymmetry in the SciPy implementations of the gamma and beta functions: there is no functions betaincc or betainccinv. These functions are unnecessary because of symmetries in the beta function. One could define betaincc(a, b, x) as betainc(b, a, 1-x) and betainccinv(a, b, x) as betaincinv(b, a, 1-x).

See also