The normal distribution is a good approximation to the Student-t distribution when the t distribution has a large degrees of freedom parameter ν. Many books recommend using the normal approximation to the t distribution when ν ≥ 30.
When ν = 30, the maximum difference between the CDFs of the normal and t distribution is 0.005244. That means that the maximum absolute error in computing the probability of any interval [a, b] by subtracting the CDF values at the two ends is going to be small. But the relative error may be enormous.
This problem of large relative error is not limited to the t distribution but is typical of normal approximations in general. The normal distribution has very thin tails, and in most applications the normal will be used to approximate a distribution with thicker tails. In that case the relative error in the normal approximation will be large in the tails.
Let GN be the CCDF of a standard normal random variable and let Gt be the CCDF of a Student-t random variable with 30 degrees of freedom. (I use the CCDF, the complementary CDF, rather than the CDF because that makes it easier to read the graphs from left to right.) The absolute error, |GN – Gt| on the interval [0, 5] is given below.
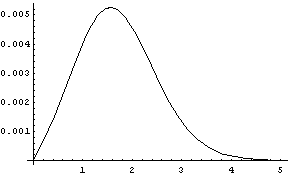
As mentioned above, the absolute error is 0.005244. The absolute error decreases as the argument |GN(x) – Gt(x)| decreases as x increases past the location of the maximum error.
The relative error curve, |GN – Gt| / Gt is very different.
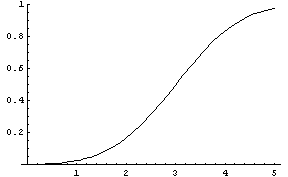
The relative error |GN(x) – Gt(x)| / Gt(x) increases as x increases and is practically 1 for large x. That is, the relative error is nearly 100%.
