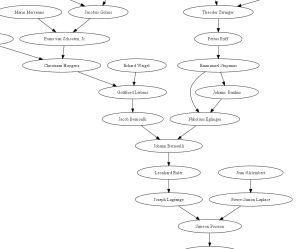
When you draw a tree of your ancestors, things quickly get out of hand. There are twice as many nodes each time you go back a generation, and so the size of paper you need grows exponentially. Things also get messy because typically you know much more about some lines than others. If you know much about your ancestry, one big tree isn’t going to work.
There’s a simple solution to this problem, one commonly used in genealogy: assign everyone in the tree a number, starting with yourself as 1. Then follow two simple rules:
- The father of person n has number 2n.
- The mother of person n has number 2n + 1.
You can tell where someone fits into the tree easily from their number. Men have even numbers, women odd numbers. The number of someone’s child is half their number (rounding down if you get a fraction). For example, person 75 on your tree must be a woman. Her husband would be 74, her child 37, her father 150, etc.
Taking the logarithm base 2 tells you how many generations back someone is. That is, person n is ⌊ log2n ⌋ generations back. Going back to our example of 75, this person would be 6 generations back because log2 75 = 6.2288. (Here ⌊ x ⌋ is the “floor” of x, the largest integer less than x. Using the same notation, the child of n is ⌊ n/2 ⌋.)
Said another way, the people m generations back have numbers 2m through 2m+1 – 1. Your paternal line has numbers equal to powers of 2, and your maternal line has numbers one less than powers of 2.
If you write out a person’s number in binary, you stick a 0 on the end to find their father and a 1 on the end to find their mother. So your paternal grandmother, for example, would have number 101 in binary. Start with your number: 1. Then tack on a zero for your father: 10. Then tack on a 1 for his mother: 101.
In our example of 75 above, this number is 1001011 in binary. Leave off the one on the left, then read from left to right saying “father” every time you see a 0 and “mother” every time you see a 1. So person 75 is your father’s father’s mother’s father’s mother’s mother.
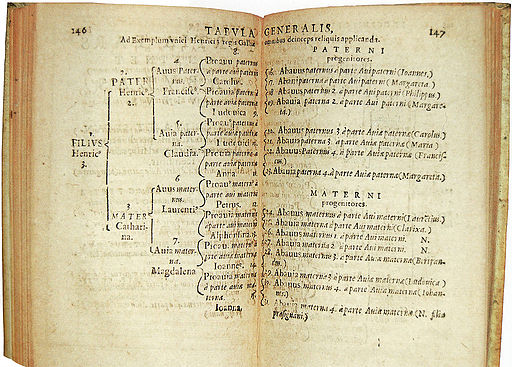
This numbering system goes back to at least 1590. In that year Michaël Eytzinger published the chart in the image above, giving the genealogy of Henry III of France.