This page presents a couple diagrams that make it easier to remember identities between trig functions (circular function) and hyperbolic trig functions (hyperbolic functions).
Circular functions
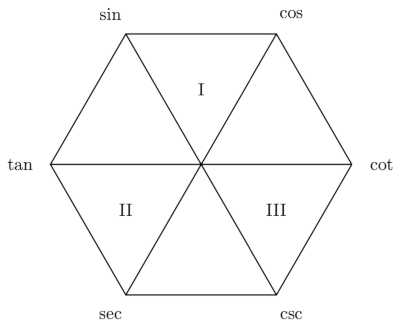
This diagram has the following properties.
- Functions and cofunctions are on horizontal lines.
- Derivatives of functions on the right have a negative sign; those on the left do not.
- Functions and reciprocals are on diagonal lines.
- Each function is the ratio of the next two functions clockwise.
- Each function the the product of its two neighbors.
- The two functions at the top are bounded. The rest are unbounded.
- The functions that are vertices of a triangle with a Roman numeral inside are related by Pythagorean identities.
The Pythagorean identities are
Hyperbolic functions
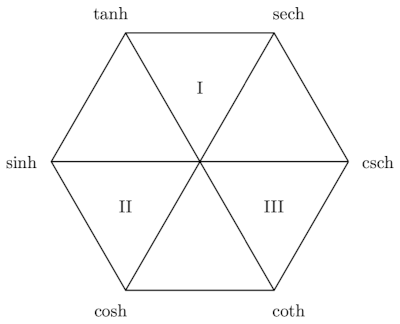
This diagram has all the properties of the previous diagram except for the first.
-
- Function and cofunctions are on lines that make a 120° angle with the horizontal.
- Derivatives of functions on the right have a negative sign; those on the left do not.
- Functions and reciprocals are on diagonal lines.
- Each function is the ratio of the next two functions clockwise.
- Each function the the product of its two neighbors.
- The two functions at the top are bounded. The rest are unbounded.
- The functions that are vertices of a triangle with a Roman numeral inside are related by Pythagorean identities.
The Pythagorean identities for hyperbolic trig functions are
If you rotate the hexagon counterclockwise 60° you can recover the first property of circular functions, but you lose the second and sixth properties.
Provenance
I found these diagrams in the article Notes on Circular and Hyperbolic Functions by William S. McCulley, Mathematics Magazine, Vol. 31, No. 1 (Sept–Oct 1957), pp. 33–38.
McCulley says that the first diagram first appeared “in the preface to Wentworth & Smith’s Trigonometry, published in the early 1920’s.” I’ve found several trigonometry books by Wentworth and Smith on the Internet Archive, some published before the 1920’s and some after, but none published in the 1920’s, and none have McCulley’s diagram.
I created the diagrams above with this LaTeX file. Here is an PDF version. Use these files however you wish.
