Programming languages are inconsistent in their support for trig functions, and inconsistent in the names they use for the functions they support. Several times I’ve been irritated by this and said that I should make a comparison chart someday, and today I finally did it.
Here’s the chart. The C column also stands for languages like Python that follow C’s conventions. More on this below.
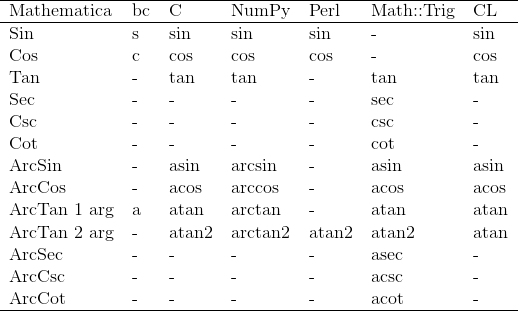
The table above is a PNG image. An HTML version of the same table is available here.
The rest of the post discusses details and patterns in the table.
Introduction
There are six trig functions according to the most common convention: sine, cosine, tangent, secant, cosecant, and cotangent. Your list could be longer or shorter, depending on how you count them. These six functions have inverses (over some range) and so a math library could have 12 trig functions, including inverses.
Except there’s a wrinkle with the inverse tangent. For any given t there are infinitely many angles θ whose tangent is t. Which one do you want? By convention, we usually want θ between -π/2 and π/2. But it’s handy sometime to specify a point (x, y) and ask for the angle made by the line from the origin to the point. In that case we a value of θ in the same quadrant as the point. So if y/x = z, the one-argument form of inverse tangent depends only on z, but the two-argument depends on both x and y; two points with equal ratios may result in different choices of θ.
So with our two versions on inverse tangent we have a total of 13 functions. This post will explain which of these 13 functions are supported in C, Python, R, Perl, Mathematica, bc, and Common Lisp, and how the supported functions are named.
Mathematica
Of the languages I looked at, only Mathematica implements all 13 functions. The names of the six basic functions are what you’d see in a contemporary calculus textbook except that, like all functions in Mathematica, names begin with a capital letter.
So the six trig functions are Sin, Cos, Tan, Sec, Csc, and Cot. The inverse functions are the same with an Arc prefix: ArcSin, ArcCos, etc.
The two inverse tangent functions are both named ArcTan. With one argument, ArcTan[z] returns an angle θ between -π/2 and π/2 such that tan θ = z. With two arguments, ArcTan[x, y] returns an angle θ in the same quadrant as (x, y) with tan θ = y/x.
C, Python, and R
Python and R follow C’s lead, as do other programming languages such as JavaScript.
C does not support sec, csc, and cot, presumably because they’re simply the reciprocals of cos, sin, and tan respectively. It does not support their inverses either.
Inverse trig functions are denoted with an a prefix: asin, acos, atan. The two-argument form of inverse tangent is atan2. The order of arguments to atan2 differs from that of Mathematica and is discussed in the section on Common Lisp below.
NumPy
NumPy supports the same trig functions as base Python, but it uses different names for inverse functions. That is, NumPy uses arcsin, arccos, arctan, and arctan2 while Python’s standard math module uses asin, acos, atan, and atan2.
Common Lisp
Common Lisp is the same as C except for the inverse tangent function of two arguments. There CL is similar to Mathematica in that the same name is used for the function of one argument and the function of two arguments.
However, the order of the arguments is reversed in CL relative to Mathematica. That is, (atan y x) in CL equals ArcTan[x, y] in Mathematica.
Even though the two languages use opposite conventions, there are good reason for both. Mathematica interprets the arguments of ArcTan[x, y] as the coordinates of a point, written in the usual order. Common Lisp interprets (atan y x) as a function whose second argument defaults to 1.
Mathematica has the advantage that the coordinates of a point are listed in the natural order. Common Lisp has the advantage that the meaning of the first argument does not change if you add a second argument.
C and languages like Python and R that follow C use the same convention as Common Lisp, i.e. the first argument to atan2 is the second coordinate of a point.
Perl
The base Perl language only supports three trig functions: sine, cosine, and two-argument inverse tangent. The module Math::Trig supports everything else, including the reciprocal functions and their inverses.
It’s interesting that Perl made the choices that it did. There are languages, like bc discussed below, that support inverse tangent of with one argument but not two; Perl is the only language I know of that does the opposite, supporting inverse tangent with two arguments but not one. It makes sense that if you’re only going to support one, you support the more general of the two.
Perl’s atan2 function uses the same argument convention as C et al., i.e. atan2(y, x), numerator first.
In the Math::Trig module, the reciprocal trig functions are named sec, csc, and cot, as is standard now. (You may see things like cosec and ctn in older math books.) Inverse functions have an a prefix, as they do in C.
There’s one inexplicable quirk in Math::Trig: the functions sin and cos aren’t there, but atan2 is. I could see leaving out sin and cos because they’re redundant with base Perl, but so is atan2. It would be more consistent to add sin and cos (my preference) or take out atan2.
bc
The Unix calculator bc has a minimal set of trig functions: sine, cosine, and (one-argument) inverse tangent. These are denoted simply s, c, and a. But you can bootstrap your way from these three functions to all the rest.
Hyperbolic functions
Hyperbolic functions essentially follow the patterns above with an “h” tacked on the end. For example, Mathematica has ArcTanh, NumPy has arctanh, while C and R have atanh.

This led me to think about trig abbreviations in other languages. For example, even though the terms are nearly identical (they come from Latin), the French abbreviations for the six standard trig functions are traditionally sin, cos, tg, cosec, sec, cotg, though in recent years most people have been adopting the English abbreviations.
I use Julia quite a bit. Julia implements all of the trig functions and their inverses (in the first column of the table).
Just for completeness, I thought I’d add APL to the list…
In APL there’s the “circle function” written as ○ (in html, it’s ○).
In its monadic form (only accepting a right-argument) it returns n times Pi.
Example: ○1 returns 3.141592654
○3J2 returns 9.424777961J6.283185307
To get to the trig functions, we need call it as a dyadic function i.e. supply a left-argument.
Now, the left-argument can be any integer from -12 to 12 so there are 25 functions in one little symbol.
But only 15 of them are Circular, Hyperbolic or Pythagorean. The remaining 10 deal with complex numbers.
Before we plunge into the list, I need to tell you about APL’s “high-minus” written as ¯ (html ¯).
¯5 means negative five, where as -5 means negative one times five. The first is a sign, the second a function.
0○x returns sqrt(1-x^2)
1○x returns Sine x
2○x returns Cosine x
3○x returns Tangent x
4○x returns sqrt(1+x^2)
5○x returns Sinh x
6○x returns Cosh x
7○x returns Tanh x
¯1○x returns Arcsin x
¯2○x returns Arccos x
¯3○x returns Arctan x
¯4○x returns sqrt(x^2 – 1)
¯5○x returns Arcsinh x
¯6○x returns Arccosh x
¯7○x returns Arctanh x
For the following calls, x is a complex numbers
8○x returns -sqrt(x^2-1) if x>=0 or sqrt(x^2-1) if x<0
9○x returns Real x
10○x returns Magnitude x
11○x returns Imaginary x
12○x returns Phase x
¯8○x returns -(8○x)
¯9○x returns x
¯10○x returns Conjugate x
¯11○x returns 0J1*x
¯12○x returns e^(0J1*x)
Perhaps worth mentioning that C is actually in the Fortran family.
C uses the Fortran names for the trig and hyperbolic trig functions.