Textbooks say the normal approximation to the binomial distribution is good when “n is large.” How large is large enough? Some books say n ≥ 10. How good is it in that case? Hmm, it doesn’t say. The same holds for the normal approximation to the Poisson. The only advice you’re likely to see is that the approximation is better when the λ parameter is “large.”
Approximations are much more useful when you have an error bound or an error estimate, and yet I’ve never seen a textbook that gave an error bound when introducing these approximations. You’ll probably get an example or two, but nothing general. One justification for this omission is that the error bounds rely on more advanced results than could be proven in an introductory class. But the approximation result is already a rabbit out of a hat. Why not pull one more rabbit out of the hat and state an error bound?
I’m supposed to teach a math stat class in the Fall. I’ve prepared some notes looking into the details of the various approximations so I could do better than just wave my hands when presenting this material. Here are my notes for the Poisson and binomial distributions.
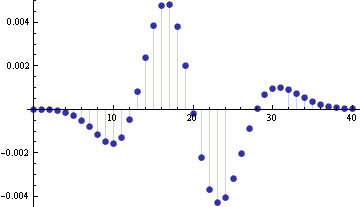
Here’s one of the graphs from the notes, an example showing the error in normal approximation to a Poisson(20) density function.

Comments are closed.