Bézier curves are very common in computer graphics. They also interesting mathematical properties. This post will give a quick introduction to Bézier curves, describing them first in visual terms and then in mathematical terms.
There are different degrees of Bézier curves: linear, quadratic, cubic, etc. Linear Bézier curves are just straight lines. The most common kind of Bézier curve in drawing programs is the cubic and that’s the one I’ll describe below.
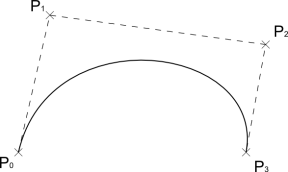
A cubic Bézier curve is determined by four points: two points determine where the curve begins and ends, and two more points determine the shape. Say the points are labeled P0, P1, P2, and P3. The curve begins at P0 and initially goes in the direction of P1. It ends at P3 going in the direction of a line connecting P2 and P3. If you move P1 further away from P0, the curve flattens, going further in the direction of P1 before turning. Similar remarks hold for moving P2 away from P3.
Now for equations. The cubic Bézier curve is given by
B(t) = (1-t)3 P0 + 3(1-t)2t P1 + 3(1-t)t2 P2 + t3 P3
for t running between 0 and 1. It’s clear from the equation that B(0) = P0 and B(1) = P3. A little calculation shows that the derivatives satisfy
B‘(0) = 3(P0 – P1)
and
B‘(1) = 3(P3 – P2).
Moving the points P1 and P2 further out increases the derivatives and thus makes the curve go further in the direction of these points before bending.
Related post: The smoothest line through a set of points

I think you might have switched the sign of the derivatives. Unless I’m mistaken, it should be B'(0)= 3(P1-P0) and B'(1) = 3(P3-P2).
Can you double check that?
Thanks. You were right. I’ve corrected the post.
You might also be interested in my Animated Bézier Curves demo.