Preview
This post will explain a connection between probability and geometry. Standard deviations for independent random variables add according to the Pythagorean theorem. Standard deviations for correlated random variables add like the law of cosines. This is because correlation is a cosine. Update: Here is a Spanish translation of this post.
Independent variables
First, let’s start with two independent random variables X and Y. Then the standard deviations of X and Y add like sides of a right triangle.
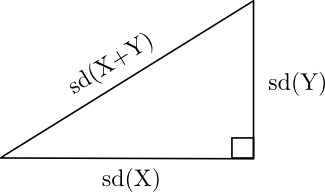
In the diagram above, “sd” stands for standard deviation, the square root of variance. The diagram is correct because the formula
Var(X+Y) = Var(X) + Var(Y)
is analogous to the Pythagorean theorem
c2 = a2 + b2.
Dependent variables
Next we drop the assumption of independence. If X and Y are correlated, the variance formula is analogous to the law of cosines.
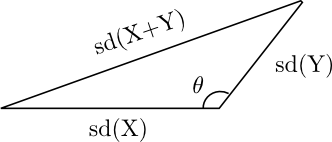
The generalization of the previous variance formula to allow for dependent variables is
Var(X+Y) = Var(X) + Var(Y) + 2 Cov(X, Y).
Here Cov(X,Y) is the covariance of X and Y. The analogous law of cosines is
c2 = a2 + b2 – 2 a b cos(θ).
If we let a, b, and c be the standard deviations of X, Y, and X+Y respectively, then cos(θ) = -ρ where ρ is the correlation between X and Y defined by
ρ(X, Y) = Cov(X, Y) / sd(X) sd(Y).
When θ is π/2 (i.e. 90°) the random variables are independent. When θ is larger, the variables are positively correlated. When θ is smaller, the variables are negatively correlated. Said another way, as θ increases from 0 to π (i.e. 180°), the correlation increases from -1 to 1.
The analogy above is a little awkward, however, because of the minus sign. Let’s rephrase it in terms of the supplementary angle φ = π – θ. Slide the line representing the standard deviation of Y over to the left end of the horizontal line representing the standard deviation of X.
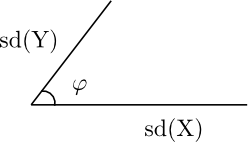
Now cos(φ) = ρ = correlation(X, Y).
When φ is small, the two line segments are pointing in nearly the same direction and the random variables are highly positively correlated. If φ is large, near π, the two line segments are pointing in nearly opposite directions and the random variables are highly negatively correlated.
Connection explained
Now let’s see the source of the connection between correlation and the law of cosines. Suppose X and Y have mean 0. Think of X and Y as members of an inner product space where the inner product <X, Y> is E(XY). Then
<X+Y, X+Y> = < X, X> + < Y, Y> + 2<X, Y >.
In an inner product space,
<X, Y > = || X || || Y || cos φ
where the norm || X || of a vector is the square root of the vector’s inner product with itself. The above equation defines the angle φ between two vectors. You could justify this definition by seeing that it agrees with ordinary plane geometry in the plane containing the three vectors X, Y, and X+Y.
Related links
{ 3 trackbacks }
{ 5 comments… read them below or add one }
Mike Anderson 06.17.10 at 06:11
Nice write-up. I sneak this into my lectures occasionally to perk up the math majors, who don’t always notice the many interesting mathematical objects that appear in statistics. ( The denominator for correlation, sd(X)sd(Y), is the geometric mean of the two variances–what’s THAT all about, guys? )
Maria Droujkova 06.17.10 at 06:37
Nice! It would only take a current events example to make a cool enrichment activity. Thank you!
Ger Hobbelt 06.17.10 at 07:30
Thank you for this; showing up right when I needed it! Alas, it would have been extra great if my teachers had pointed out this little bit of intel about 25 years ago, while they got me loathing those ever-resurfacing bloody dice even more. Meanwhile, I’ve shown to be dumb enough not to recognize this ‘correlation’ with lovely goniometrics on my own.
Despite all that I’ve found the increasing need for understanding statistics (as you work on/with statistical classifiers and you feel the need to really ‘get’ those s.o.b.s for only then do you have a chance at reasoning why they fail on you the way they do) and your piece just made a bit of my brain drop a quarter — I’m Dutch; comprehension is so precious around here we are willing to part with a quarter instead of only a penny
Harry Hendon 06.21.10 at 19:55
Hi John, maybe you can help on a related problem, which I think uses the law of cosines as well (but I lost my derivation):
If you know the two correlations of one time series with two other predictor time series, what does this tell you about the possible range of correlation between the two predictor time series. That is, given r(X,Y)=a and r(X,Z)=b, what is the possible range of r(Y,Z)=c in terms of a and b?
Of course some examples are intuitively trivial (eg, if a=b=1, then c=1, and if a=0 but b=1 then c=0). But, consider if a=b=.7 (which are strong correlations), then I think the possible range of c is still enormous (0.<c<1. ). In this case, I reasoned because X accounts for half the variance of Z and Y accounts for half the variance of Z that X could possibly account for the same half of the variance as Y (ie c=r(X,Y)=1). Or, X could account completely for the other half of the variance that is not accounted for by Y but together X and Y account for all of the variance of Z (ie c=r(X,Y)=0). This understanding has, for instance, implications for (over) interpreting causality based on empirical evidence.
Guillermo Bautista 07.04.10 at 02:47
nice article John. We’re looking for more of this.