Pick a number x between 0 and 1. Then repeatedly replace x with 4x(1-x). For almost all starting values of x, the result exhibits chaos. Two people could play this game with starting values very close together, and eventually their sequences will diverge.
It’s somewhat surprising that the iterative process described above can be written down in closed form. Starting from a value x0, the value after n iterations is
sin( 2n arcsin( √ x0 ) )2.
Now suppose two people start with the same initial value. One repeatedly applies 4x(1-x) and the other uses the formula above. If both carried out their calculations exactly, both would produce the same output at every step. But what if both used a computer?
The two approaches correspond to the Python functions f and g below. Because both functions are executed in finite precision arithmetic, both have errors, but they have different errors. Suppose we want to look at the difference between the two functions as we increase n.
from scipy import arcsin, sin, sqrt, linspace
from matplotlib import pyplot as plt
def f(x0, n):
x = x0
for _ in range(n):
x = 4*x*(1-x)
return x
def g(x0, n):
return sin(2.0**n * arcsin(sqrt(x0)))**2
n = 40
x = linspace(0, 1, 100)
plt.plot(x, f(x, n) - g(x, n))
plt.ylim(-1, 1)
plt.show()
When we run the code, nothing exciting happens. The difference is a flat line.
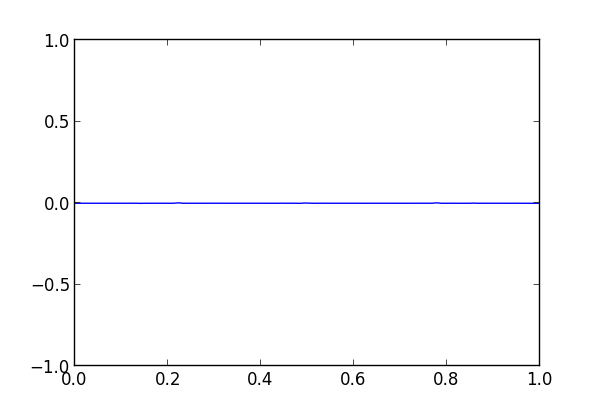
Next we increase n to 45 and we start to see the methods diverge.
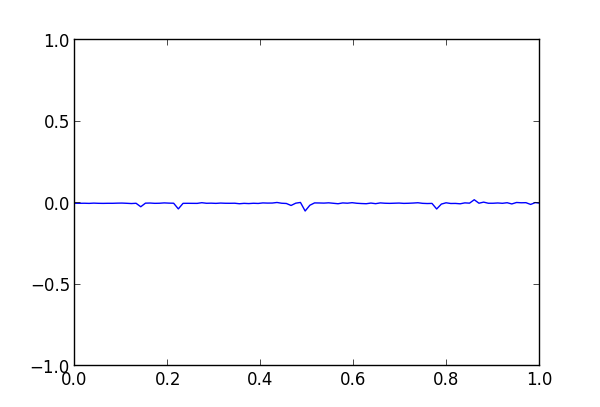
The divergence is large when n is 50.
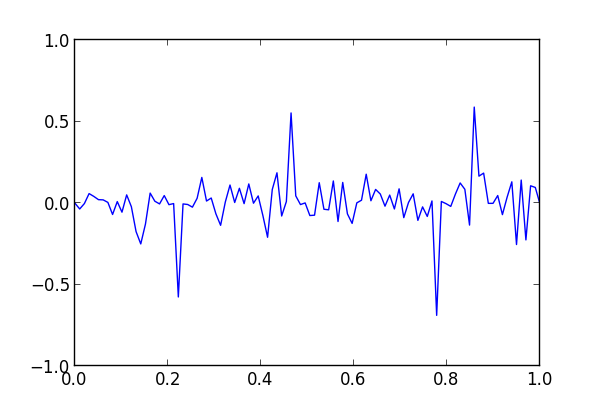
And the two functions are nearly completely uncorrelated when n is 55.
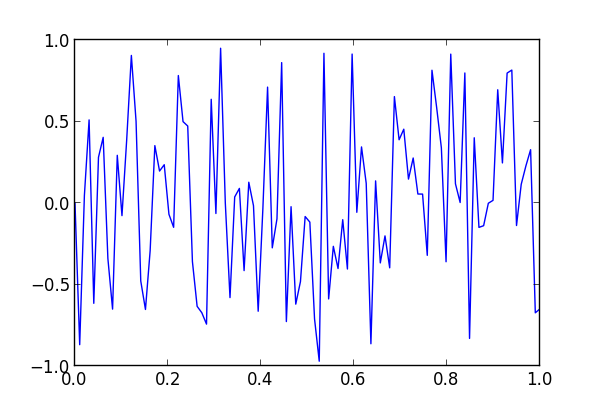
Update
So which function is more accurate, f or g? As noted in the comments, the two functions have different kinds of numerical errors. The former accumulates arithmetic precision error at each iteration. The latter shifts noisy bits into significance by multiplying by 2^n. Apparently both about the same overall error, though they have different distributions of error.
I recomputed g using 100-digit precision with mpmath and used the results as the standard to evaluate the output of f and g in ordinary precision. Here’s a plot of the errors when n = 45, first with f
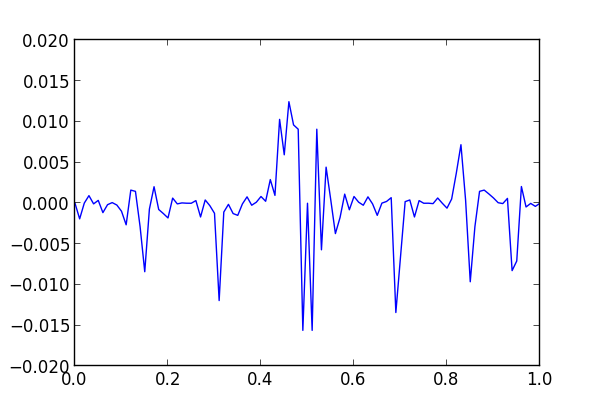
and then with g.
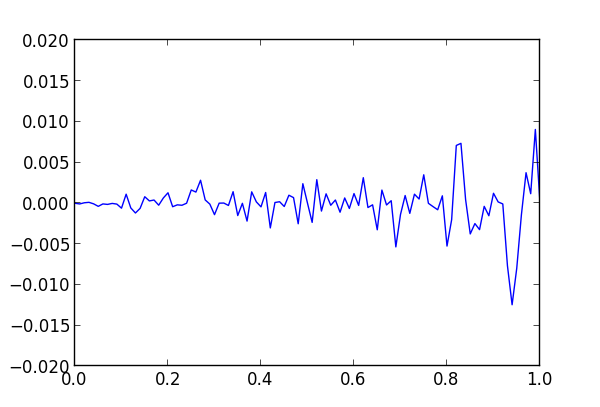
The average absolute errors of f and g are 0.0024 and 0.0015 respectively.

In the end, this boils down to http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
Thomas: I think that’s part of it. The limitations of floating point explain why things fall apart at around n = 50, approximately the number of bits of precision in a floating point number. But there are other functions you could iterate thousands of times with no floating point problems because their iterates are not chaotic.
John: OK, so when you have a non-chaotic iteration, then h(n) = |f(n) – g(n)| should increase monotonically instead of just being a chaotic function itself for large enough n. (just some wild guess).
Thomas: It depends on the function being iterated. If the function is a contraction, then |f – g| would get smaller over time because both f and g would become more accurate.
Part of what’s going on here is that the two functions have different kinds of numerical error. The function f loses precision from simple arithmetic. The sine formula loses precision due to shifting. When you multiply the argument of sine by 2^n, you’re making noisy bits significant.
John: Yes, I forgot about contractions et al. I get your point now, I was just skimming the post and then thought to myself, that it’s just another floating point error. But in fact, it’s more than that.
Now, I wonder which version is closer to the “real” value. It probably is the closed form, but when you get to large n, then 2^n squeezes out a lot of precision. On the other hand, the other version accumulates a lot of error from the iteration. Interesting …
Thomas: I updated the post to answer your question. Apparently the sine formula is better overall, but not much better and not uniformly better.
Hello John.
YMMV, but I prefer to fix the axis to the same limits when showing two graphs for comparison. Your last two graphs differ in scale in their x axis. Obviously, I can do that given that you provide the code. But I think it will help the readers to better understand the issue if you update the graphs.
Again, it is just my opinion. You blog is still awesome ;)
Anonymous: Good point. I recreated the last two figures to use the same vertical scale.
Great demonstration of sensitivity to initial conditions!
Do you think the divergnce around n=50 is due to the properties of the floating point precision (The time when first differences appear) or due to the Lyapunov exponent of the system?
Ran: Each iteration looses about a bit of precision in either method, so that’s why things fall apart around n=50. But the sensitivity of the system makes the loss of precision show up more dramatically.
John: I’m not sure I agree. Let’s say you use your high precision implementation but start from two different initial conditions that differ from one another by what would be one bit in the floating point representation, then you would still see divergence even though your calculation is “exact”.
These are two separate issues.
For chaotic systems the divergence does not rely on how fast you lose precision (in other words, the amount of noise) any two different initial conditions diverge even with infinite precision (without any noise).
All I’m saying is that the divergence may not be due to the fact that you lose too much precision…
I’m actually more interested in how you derive the closed form sine expression from the recursion. Not obvious to me at all.
Also, might the relative ‘goodness’ of these depend on how sine and arcsine are implemented in a particular programming language? Neither one is ‘exact’…
If you let T_n = sin^2(U_n), translate the recurrence into the recurrence of U_n, the rest will be obvious.
Finding a good substitution for solving non-linear recurrence is hard – if I were only given the problem, I wouldn’t be able to even guess to substitute sine squared.
Here’s a related paper: Method of constructing exactly solvable chaos.