I saw somewhere that James Earl Jones’ speaking voice is around 85 Hz. What musical pitch is that?
Let P be the frequency of some pitch you’re interested in and let C = 261.626 be the frequency of middle C. If h is the number of half steps from C to P then
P / C = 2h/12.
Taking logs,
h = 12 log(P / C) / log 2.
If P = 85, then h = −19.46. That is, James Earl Jones’ voice is about 19 half-steps below middle C, around the F an octave and a half below middle C.
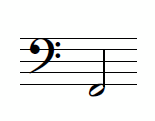
More details on the derivation above here.
There’s a page to do this calculation for you here. You can type in frequency or pitch and get the other back.
(The page also gives pitch on a Bark scale, something you may not care about that is important in psychoacoustics.)


I’m a fan of using the A above/below middle C (3 half steps or 9 half steps, respectively). Below is 220 hz, above is 440 hz. Obviously the math works out the same, and I get 16.46 half steps below the A below middle C.
Thank you very much for these posts related to music and math. If I’m not mistaken, when I compute 19 half-steps from middle C, I get F instead of F#. I checked the piano key frequencies (http://en.wikipedia.org/wiki/Piano_key_frequencies) and it also says 85 Hz is roughly F. I wonder where do I make the mistake?
You’re right. My mistake.
Since 19.46 is so close to 19.5, you could also say that it’s near to F half-flat (F
This reminds me of a problem I’ve wondered about. How do you take a piece of recorded music, and raise it an octave (or some number of semi-tones) electronically, without changing its duration? This is what Autotune does, I think. I don’t know of any clean mathematical way to do this. Intuitively it seems like something the Fourier transform was built for but I can’t get it to work out.
@SteveBrooklineMA you can try reading about phase vocoders. Here are some references:
http://sethares.engr.wisc.edu/vocoders/phasevocoder.html
The least-squares invertible constant-Q spectrogram and its application to phase vocoding, J. Acoust. Soc. Am. Volume 132, Issue 2, pp. 894-903 (2012)
James Earl Jones was awesome in Dr. Strangelove. “Negative function sir. The bomb bay doors are still closed.”