Golden strings & rabbit constant

Golden strings are analogous to Fibonacci numbers, except one uses concatenation rather than addition.

Start with s₁ = “1” and s₂ = “10”. Then define s_n = s_n-1 + s_n-2 where “+” means string concatenation.

The first few golden strings are

“1”
“10”
“101”
“10110”
“10110101”
…

The length of s_n is F_n+1, the n+1st Fibonacci number. Also, s_n contains F_n 1’s and F_n-1 0’s. (Source: The Glorious Golden Ratio).

If we interpret the s_n as the fractional part of a binary number, the sequence converges to the rabbit constant R = 0.7098034428612913…

It turns out that R is related to the golden ratio φ by

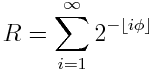
$R = \sum_{i=1}^\infty 2^{-\lfloor i \phi \rfloor}$

where ⌊i φ⌋ is the largest integer no greater than iφ.

Here’s a little Python code to print out the first few golden strings and an approximation to the rabbit constant.

    from mpmath import mp, fraction

    a = "1"
    b = "10"
    for i in range(10):
        b, a = b+a, b
        print(b)

    n = len(b)
    mp.dps = n
    denom = 2**n
    num = int(b, 2)

    rabbit = fraction(num, denom)
    print(rabbit)

Note that the code sets the number of decimal places, mp.dps, to the length of the string b. That’s because it takes up to n decimal places to exactly represent a rational number with denominator 2ⁿ.