When I solve a problem by appealing to symmetry, students’ jaws drop. They look at me as if I’d pulled a rabbit out of a hat.
I used think of these tricks as common knowledge, but now I think they’re common knowledge in some circles (e.g. physics) and not as common in others. These tricks are simple, but not as many people as I’d thought have been trained to spot opportunities to apply them.
Here’s an example.
Pop quiz 1: Evaluate the following intimidating integral.
Solution: Zero, by symmetry, because the integrand is odd.
The integrand is an odd function (i.e. f(−x) = −f(x)), and the integrand of an odd function over a symmetric interval is zero. This is because the region below the x-axis is symmetric to the region above the x-axis as the following graph shows.
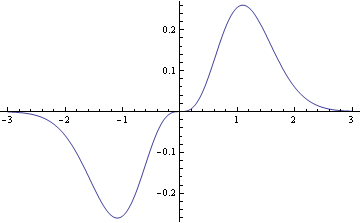
The example above is not artificial: similar calculations come up constantly in applications. For example, the Fourier series of an odd function contains only sine terms, no cosine terms. Why? The integrals to compute the Fourier coefficients for the cosine terms all involve odd functions integrated over an interval symmetric about zero.
Another common application of symmetry is evaluating derivatives. The derivative of an odd function is an even function and vice versa.
Pop quiz 2: What is the coefficient of x5 in the Taylor series of cos(1 + x2)?
Solution: Zero, by symmetry, because cos(1 + x2) is an even function.
Odd functions of x have only odd powers of x in their Taylor series and even functions have only even powers of x in their Taylor series. Why? Because the coefficients come from derivatives evaluated at zero.
If f(x) is an odd function, all of its even derivatives are odd functions. These derivatives are zero at x = 0, and so all the coefficients of even powers of x are zero. A similar argument shows that even functions have only even powers of x in their Taylor series.
Symmetry tricks are obvious in hindsight. The hard part is learning to recognize when they apply. Symmetries are harder to recognize, but also more valuable, in complex situations. The key is to think about the problem you’re trying to solve before you dive into heads-down calculation.

Your last sentence is beautifully stated and generally applicable—the very qualities that you bring to so many of your blog posts. Thanks for sharing your insights.
I’m rather taken with the function at the beginning of the post, does it come from a real application?
Cheers
Mat
But you also have to be very careful with symmetry arguments, or they can get you into a lot of trouble.
E.g. In your first example, you need to prove the integral converges before you can conclude its value is zero. (Otherwise consider e.g. integrating f(x)=x from negative to positive infinity. The same symmetry argument applies, so you might mistakenly conclude its value is zero, while in truth the integral clearly diverges.)
Rick: Thanks!
Yosef: Good point.
Mat: I’ve never seen this integral in application, but it’s plausible that it could. If you’re computing expected values of functions of normal random variables you’ll get integrals of the form f(x) exp(-x2). But as for f(x) = x log(1 + x2), I don’t know why that would come up.
Now the function log(1 – x2) does come up in applications. (Notice the change of sign.) That function is known as a “logarithmic barrier” in optimization. It’s a way to constrain a function to (0, 1) by making it blow up at the end points.
Sometimes, after solving a problem, it seems to me there should be a symmetry argument that I missed.
You have a cup of coffee and a cup of cream. Put a teaspoon of the cream in the coffee and stir. Take a teaspoon of this mixture and put it in the cream. Is there now more cream in the coffee or coffee in the cream?
Neither. It turns out that they are equal. Should this have been obvious? Why? Is there a symmetry argument?
@SteveBrooklineMA, that’s not right.. they’d be equal if you take a teaspoon from both unmixed liquids and put it in… since the teaspoon of coffee has some cream in it, less coffee ends up in the cream than you would if it were not diluted… duh?
maybe I just got nerd sniped…
The spoon of coffee has some cream in it, but you are taking it out of a mixture containing 1 cup + one spoon of liquid. It balances out exactly.
In your second example I think you mean the Maclaurin series of the function specifically, as only in that case are the derivatives evaluated at zero. Otherwise the derivatives are evaluated at whichever number the Taylor series is centered around.