After posting about a magic square made from knight’s tour, I wondered whether there are magic squares made from a king’s tour. (A king can move one square in any direction. A tour is a sequence of moves that lands on each square of a chess board exactly once.) I found George Jelliss’ site via the comments to that post and found out that there are indeed magic king’s tours. Here’s one published in 1917.
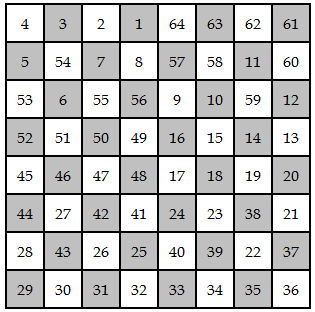
Here’s the path a king would take in the square above:
The knight’s tour magic square had rows and columns that sum to 260, though the diagonals did not. In fact, someone has proved that a knight’s tour on an 8×8 board cannot be diagonally magic. (Thanks John V.)
In the king’s tour above, however, the rows, columns, and diagonals all sum to 260. George Jelliss has posted notes that classify all such magic squares that have biaxial symmetry. See his site for much more information.
{ 1 trackback }
{ 4 comments… read them below or add one }
Usov 04.13.11 at 17:55
Omg, how do they construct them? Are there any smarter ways beyond brute force search? I can’t imagine how much time it would take to do direct search manually.
Daniel Lemire 04.13.11 at 20:58
@Usov Clearly the solution here has some symmetry, so it could be deduced without brute force.
Usov 04.14.11 at 04:21
You mean he had to brute-force just 1/8 of a desk. Which saves quite a bit of work.
Craig Knecht 05.17.11 at 08:51
Hi John,
Thanks for the post on the magic square king’s tour. I have been fooling around with some magic square models. I made a 3D water retention graphic of your kings tour.