Degree of magic

Posted on 8 December 2021 by John

A square grid of distinct integers is a magic square if all its rows columns and full diagonals have the same sum. Otherwise it is not a magic square.

Now suppose we fill a square grid with samples from a continuous random variable. The probability that the entries are distinct is 1, but the probability that the square is magic is 0.

We could make this more interesting by asking how close to magic the square is, using a continuous measure of degree of magic, rather than simply asking whether the square is magic or not.

If we have an n by n square of real numbers, we could take the set of n row sums, n column sums, and 2 diagonals as data and look at its range or its variance. These statistics would be zero for a magic square and small for a nearly magic square.

If each element of the square is a sample from a standard normal random variable, what is the distribution of these statistics? How much does the distribution on the numbers matter?

Magic square of squares

Posted on 20 April 2021 by John

Allen William Johnson [1] discovered the following magic square whose entries are all squares.

$\begin{bmatrix} 30^2 & 246^2 & 172^2 & 45^2 \\ 93^2 & 116^2 & 66^2 & 258^2 \\ 126^2 & 138^2 & 237^2 & 44^2 \\ 260^2 & 3^2 & 54^2 & 150^2 \\ \end{bmatrix}$

The following Python code verifies that this is a magic square.

    import numpy as np
    
    M = np.array(
        [[ 30**2, 246**2, 172**2,  45**2],
         [ 93**2, 116**2,  66**2, 258**2],
         [126**2, 138**2, 237**2,  44**2],
         [260**2,   3**2,  54**2, 150**2]
        ])
    
    def verify(M):
    
        m, n = M.shape
        assert(m == n)
    
        c = sum(M[0, :])
        semimagic = True
        for i in range(m):
            semimagic &= sum(M[i,:]) == c
            semimagic &= sum(M[:,i]) == c
    
        d1 = sum(M[i, i  ] for i in range(m))
        d2 = sum(M[i,-i-1] for i in range(m))
        magic = semimagic and (d1 == d2 == c)
    
        if magic:
            return "magic"
        if semimagic:
            return "semi-magic"
        return "not magic"
    
    print(verify(M))

Three things about dominoes

Posted on 19 June 2018 by John

Here are three things about dominoes, two easy and one more advanced.

Counting

First, how many pieces are there in a set of dominoes? A domino corresponds to an unordered pair of numbers from 0 to n. The most popular form has n = 6, but there are variations with other values of n. You can show that the number of dominoes is

${ n+1\choose 2} + n + 1$

This is because there are n+1 possible numbers (since blanks are a possibility) and each one is either a double or not. The number of ways to choose two distinct numbers is the binomial coefficient and the number of doubles is n+1.

Another way to look at this is that we are selecting two things from a set of n+1 things with replacement and so the number of possibilities is

$\left({ n+1\choose 2}\right) = {n+2 \choose 2}$

where the symbol on the left is Stanley’s symbol for selection with replacement.

In any case, there are 28 dominoes when n = 6, 55 when n = 9, and 91 when n = 12.

Magic squares

There are a couple ways to make a magic square of sorts from a set of dominoes. To read more about this, see this post.

Domino magic square

Tiling

How many ways can you cover an m by n chess board with dominoes? The answer turns out to be

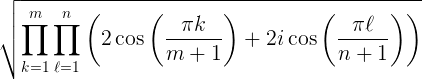
$\sqrt{\prod_{k=1}^m \prod_{\ell=1}^n \left( 2\cos\left(\frac{\pi k}{m+1} \right) + 2i \cos\left(\frac{\pi \ell}{n+1} \right) \right)}$

See this post for details.

Magic squares as matrices

Posted on 20 January 2018 by John

If you view a 3 × 3 magic square as a matrix and raise it to the third power, the result is also a magic square.

More generally, if you multiply an odd number of 3 × 3 magic squares together, the result is a magic square.

For example, here are three magic squares that appeared in my blog post on Spanish magic squares, and you can verify that their product is another magic square.

$\left[ \begin{array}{ccc} 93 & 155 & 121 \\ 151 & 123 & 95 \\ 125 & 91 & 153 \\ \end{array} \right] \left[ \begin{array}{ccc} 12 & 21 & 15 \\ 19 & 16 & 13 \\ 17 & 11 & 20 \\ \end{array} \right] \left[ \begin{array}{ccc} 13 & 20 & 18 \\ 22 & 17 & 12 \\ 16 & 14 & 21 \\ \end{array} \right] = \left[ \begin{array}{ccc} 299622 & 301968 & 301722 \\ 303204 & 301104 & 299004 \\ 300486 & 300240 & 302586 \\ \end{array} \right]$

Source: Martin Gardner, Some New Discoveries About 3 × 3 Magic Squares, Math Horizons, February 1998.

The same article conjectures that the results above are true for magic squares of any odd order. That was 20 years ago. Maybe the conjecture has been resolved by now. If you know, please leave a comment.

Consecutive pair magic square

Posted on 25 April 2016 by John

The following magic square has a couple unusual properties. For one, numbers appear in consecutive pairs. Also, you can connect the numbers 1 through 32 in a continuous path.

I found this in Before Sudoku. The authors attribute it to William Mannke, “A Magic Square.” Journal of Recreational Mathematics. 1 (3) page 139, July 1968.

Other magic squares:

Chess themed: Knight, King
Planet themed: Jupiter, Mars
Language themed: Spanish, French

Magic hexagon

Posted on 11 April 2016 by John

The following figure is a magic hexagon: the numbers in any straight path through the figure add to 38, even though paths may have length three, four, or five.

I found this in Before Sudoku. The authors attribute it to Madachy’s Mathematical Recreations.

This is essentially the only magic hexagon filled with consecutive integers starting with one. The only others are rotations or reflections of this one, or the trivial case of a single hexagon.

Magic square posts

Mars, magic squares, and music
Alphamagic squares in English, French, and Spanish

Magic square rows and columns as numbers

Posted on 5 April 2016 by John

Take any 3 by 3 magic square. For example, here’s the ancient Lo Shu square:

[[4,9,2],[3,5,7], [8,1,6]]

If you read the rows as numbers and sum their squares, you get the same thing whether you read left to right or right to left. In this case

492² + 357² + 816² = 294² + 753² + 618².

Similarly, if you read the columns as numbers and sum their squares, you get the same thing whether you read top to bottom or bottom to top:

438² + 951² + 276² = 834² + 159² + 672².

This doesn’t depend on base 10. It’s true of any base. And the entries of the magic square do not have to be single digits as long as you take the first to be the coefficient of b², the second the coefficient of b, and the last the coefficient of 1, where b is your base.

In addition to rows and columns, you can get analogous results for diagonals.

456² + 978² + 231² = 654² + 879² + 132²

456² + 312² + 897² = 654² + 213² + 798²

258² + 936² + 471² = 852² + 639² + 174²

258² + 714² + 693² = 852² + 417² + 396²

How would you prove this? Arthur Benjamin and Kan Yasuda give an elegant proof here using permutation matrices. Or you could use brute-force starting with Édouard Lucas’ theorem that every 3 by 3 magic square has the following form.

[[c-b, c+a+b, c-a], [c-a+b, c, c+a-b], [c+a, c-a-b, c+b]]

(For each a, b, and c there are eight variations on magic square given by Lucas, reflections and rotations of his square.)

Benjamin and Yasuda attribute this discovery to R. Holmes in 1970. “The magic magic square”, The Mathematical Gazette, 54(390):376.

Alphamagic squares in French

Posted on 3 April 2016 by John

In earlier blog posts I give examples of alphamagic squares in English and in Spanish. This post looks at French.

French flag

The Wikipedia article on alphamagic squares, quoting The Universal Book of Mathematics, says

French allows just one 3 × 3 alphamagic square involving numbers up to 200, but a further 255 squares if the size of the entries is increased to 300.

My script did not find a French alphamagic with entries no larger than 200, but it did find 254 squares with entries no larger than 300. (For each of these squares there are 7 more variations you can form by rotation and reflection.)

The French alphamagic square with the smallest maximum entry that I found is the following.

[[3, 204, 102], [202, 103, 4], [104, 2, 203]]

When spelled out in French we get

[[trois, deux cent quatre, cent deux], [deux cent deux, cent trois, quatre], [cent quatre, deux, deux cent trois]]

And when we replace each cell with its number of letters we get the following magic square:

[[ 5, 14, 8], [12, 9, 6], [10, , 13]]

A list of all the French magic squares with maximum element 300 that I found is available here.

Alphamagic square in Spanish

Posted on 3 April 2016 by John

In a previous post I gave an example of an alphamagic square in English. This is a magic square such that if you replace each number with the letter count when spelling out the word, you get another magic square.

Flag of Spain

I wondered whether I could find an alphamagic square in Spanish, so I wrote a script to look. I found two. (Plus there are eight rotations and reflections of each.)

The first is the following:

[[93, 155, 121], [151, 123, 95], [125, 91, 153]]

When spelled out in Spanish the numbers are:

[[noventa y tres, ciento cincuenta y cinco, ciento veintiuno], [ciento cincuenta y uno, ciento veintitrés, noventa y cinco], [ciento veinticinco, noventa y uno, ciento cincuenta y tres]]

And the number of letters in each cell gives:

[[12, 21, 15],[19, 16, 13], [17, 11, 20]]

Here’s a second example:

[[95, 156, 124], [154, 125, 96], [126, 94, 155]]

Spelled out in Spanish:

[[noventa y cinco, ciento cincuenta y seis, ciento veinticuatro], [ciento cincuenta y cuatro, ciento veinticinco, noventa y seis], [ciento veintiséis, noventa y cuatro, ciento cincuenta y cinco]]