When asked why he robbed banks, Willie Sutton famously replied “Because that’s where the money is.”
If you read about data analysis in high dimensions, you might hear someone say they’re focused on a thin shell because that’s where the probability is. For a multivariate normal distribution in high dimensions, nearly all the probability mass is concentrated in a thin shell some distance away from the origin.
What does that mean? Why is it true? How thin is the shell and what is its radius?
It seems absurd to say the probability is concentrated in a shell. The multivariate normal density has its greatest value at the origin and quickly decays as you move out in any direction. So most of the probability must be near the origin, right? No, because mass equals density times volume. The density decays quickly as you move away from the origin, but volume increases quickly. The product of the two is greatest at some radius away from the origin. That’s the shell.
The volume of a sphere in d dimensions is proportional to rd, so volume increases very quickly if d is large. For example, if d = 100, how much of the volume of a unit sphere is between a distance of 0.99 and 1 from the origin? Since 1100 – 0.99100 = 0.634, this says 63.4% of the volume is in the outer shell of thickness 0.01.
Since volume of a sphere is proportional to rd, the volume of a shell of radius r and thickness Δr is roughly proportional to d rd-1 Δr. When you multiply that volume by the probability density exp( –r2 / 2 ) you get that the probability mass in the shell is proportional to
rd-1 exp( –r2 / 2 ) Δr.
This leads to a χ distribution with d degrees of freedom. (Not the better known χ2 distribution.) This distribution has mode √(d-1) and variance 1. For large d, the distribution is approximately normal. So a multivariate normal in d dimensions with d large has roughly 95% of its probability mass in a shell of radius √d with thickness 4, two standard deviations either side of √d. (I’m approximating anyway, so I approximated √(d-1) as √d to make the conclusion a little simpler.)
The graph below gives the probability density of shells as a function of radius in dimensions 10 and 100.
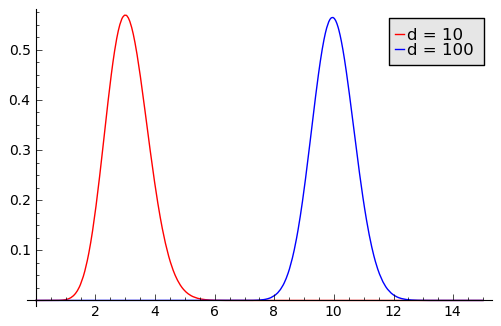
Related post: Volumes of Lp unit balls

Interesting. If you take N independent samples from a standard normal with N huge, the sample mean will likely be very close to zero. The sample standard deviation will likely be very close to sqrt(N), i.e. within a small percentage. Thus the N-variate normal is highly concentrated around the sqrt(N)-shell.
Similarly, if you fill a huge NxN matrix M with independent samples from a standard normal, M^t*M will be close to N*Identity. Thus random points selected uniformly at random from the sphere in N dimensions are likely to be nearly orthogonal.
I thought this one up but haven’t tried it yet:
Does there exist a multivariate distribution (whose tails must fall faster than the Normal I assume) in which the projection of every 2d plane containing the origin keeps the resultant distribution Uniform (over the d-ball of radius 1)? Is it well known?
First the Uniform distribution implies equal areas map to equal probability mass.
I believe my “every 2d plane” criteria is equivalent to saying every Δr thickness shell has a probability mass proportional to r^2, since the volume of the shell must mapped into the equivalent probability mass of a Δr shell in a 2d a Uniform distribution over the unit circle. With that and the symmetry constraint, then the solution follows. Haven’t worked out the algebra to see if that is some well known distribution.