Don Fredkin left a comment on my previous blog post that surprised me. I found out that latitude doesn’t exactly mean what I thought.
Imagine a line connecting your location with the center of the Earth. I thought that your latitude would be the angle that that line makes with the plane of the equator. And that’s almost true, but not quite.
Instead, you should imagine a line perpendicular to the Earth’s surface at your location and take the angle that that line makes with the plane of the equator.
If the Earth were perfectly spherical, the two lines would be identical and so the two angles would be identical. But since the Earth is an oblate spheroid (i.e. its cross-section is an ellipse) the two are not quite the same.
The angle I had in mind is the geocentric latitude ψ. The angle made by a perpendicular line and the plane of the equator is the geographic latitude φ, also known as the astronomical latitude. The following drawing from Wikipedia illustrates the difference, exaggerating the eccentricity of the ellipse.
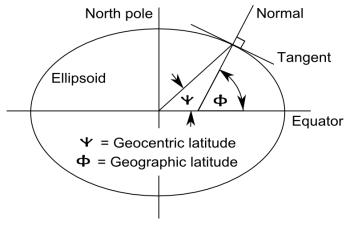
How do these two ideas of latitude compare? I’ll sketch a derivation for equations relating geographic latitude φ and geocentric latitude ψ.
Let f(x, y) = (x/a)2 + (y/b)2 where a = 6378.1 km is the equatorial radius and b = 6356.8 km is the polar radius.. The gradient of f is perpendicular to the ellipse given by the level set f(x, y) = 1. At geocentric latitude ψ, y = tan(ψ) x and so the gradient is proportional to (1/a2, tan(ψ) / b2). From taking the dot product with (1, 0) it follows that the cosine of φ is given by
(1 + (a/b)4 tan2 ψ)−1/2.
It follows that
φ = tan−1( (a/b)2 tan ψ )
and
ψ = tan−1( (b/a)2 tan φ ).
The geocentric and geographic latitude are equal at the poles and equator. Between these extremes, geographic latitude is larger than geocentric latitude, but never by more than 0.2 degrees. The maximum difference, as you might guess, is near 45 degrees.
Here’s a graph of φ − ψ in degrees. The difference between these two angles is called the angle of vertical.
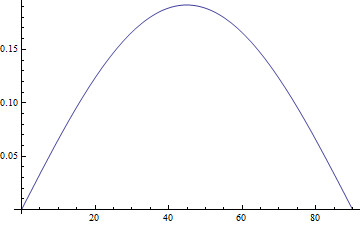
The maximum occurs at 44.9 degrees and equals 0.1917.
The curve looks very much like a parabola, and indeed it is. The approximation
φ = ψ + 0.186 − 0.0000946667 (ψ − 45)2
is very accurate, within about 0.005 degrees.
Related post: Journey away from the center of the Earth

Also the commonly used “30 degrees north Latitude” is actually Co-Latitude. Another surprise in something you thought you knew since grade school.
Very interesting!
What an eye-opener!
have you heard of the rhumb line? i would like to believe that all this talk about Fibonacci numbers in nature could actually be explained by it:
http://en.wikipedia.org/wiki/Rhumb_line
Nice article. You have quite an interesting blog. I’m subscribing!
BTW, have you considered using MathJax to display equations in web pages?
That’s quite an eccentric ellipse (Although the earth does spin fairly quickly)! Although the differences are small, it’s useful information to know and you’ve explained it well.
I think the term “geodetic latitude” is actually more common than “geographic latitude”.
Hmm. That is very interesting. I would bet that until people realized that the earth was not a sphere they used the geocentric latitude while thinking of it as the geographic latitude, because on a sphere they are the same and using a plumb bob or level is easier than trying to ascertain the tangent plane to the surface. I guess the place the difference would show up would be in the conversion of latitude to distance, but just playing around with the numbers it looks like the difference in North-South surface distance between two points calculated from either kind of latitude is very small.
It seems, there is a typos. Please look at my notes.