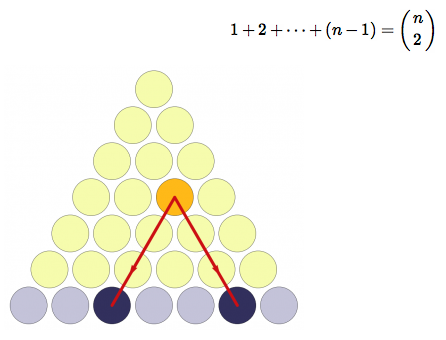
There are as many yellow dots above the bottom row of the triangle as there are pairs of purple dots on the bottom row. To see this, note that every yellow dot determines a pair of purple dots by projecting it down to the left and to the right. Conversely, you can go up from any pair of purple dots up to a yellow dot.
Via sark
Related post: Tetrahedral numbers

heh that’s the sort of thing i would expect to see in TAOCP
This looks very close to Triangular Numbers ( http://en.wikipedia.org/wiki/Triangular_number) and I also feel that it can be used to explain that if particular problem pattern falls into a Triangular number order, then it’s complexity grows n^2. n being the final row, you will end up increasing the number of yellow dots in the top triangle.
Nice! Perhaps leave out ‘in the top of the triangle’ or replace it with ‘above the bottom row’.
gabe: Good idea. I took your suggestion.
I didn’t understand how the sequence-sum explains the pair-counting property.
BTW, doesn’t sequence sum equals N*(N-1)/2?
Regarding triangular numbers, it makes perfect sense sense as the number of dots above the bottom row is simply the previous triangular number.
I really like “Proofs without words” [1]. Thanks!
[1] There are a couple of books with that name, I think with proofs like the one here. There are details at the bottom of: http://en.wikipedia.org/wiki/Proof_without_words
If you add an upside down copy of the yellow triangle next to the original one to form a parallelogram, then you can also see at a glance that the there are n*(n-1)/2 yellow dots.