A few months ago I wrote about suffix primes, prime numbers such that all their “suffixes” are prime. For example, 653 is prime, and it’s a suffix prime because 53 and 3 are primes.
James Griffin pointed out that the primes have a natural tree structure, the parent of each number being that number with its most significant digit removed. There are two separate trees: one for numbers ending in 3 and another for numbers ending in 7. The numbers 2 and 5 are isolated nodes with no descendants.
There are 4260 suffix primes, about half ending in 3 and half ending in 7. A full list is available here. The graph of either tree is a mess, but here we show the first three levels of the graph for numbers ending in 3.
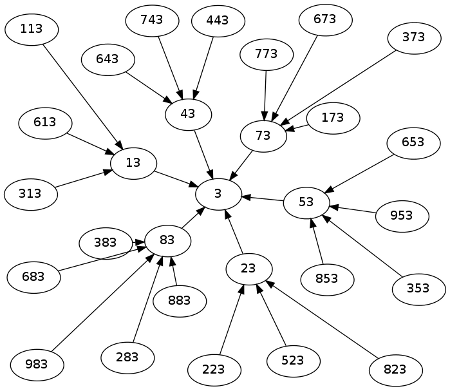
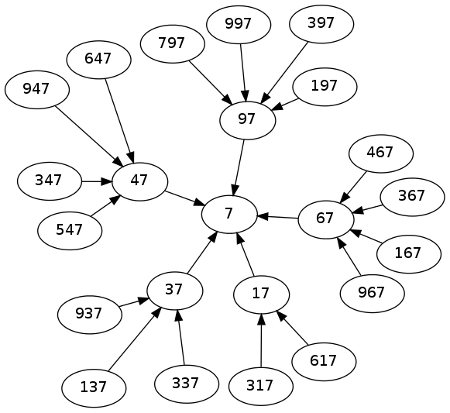
And here’s the corresponding graph for numbers ending in 7.
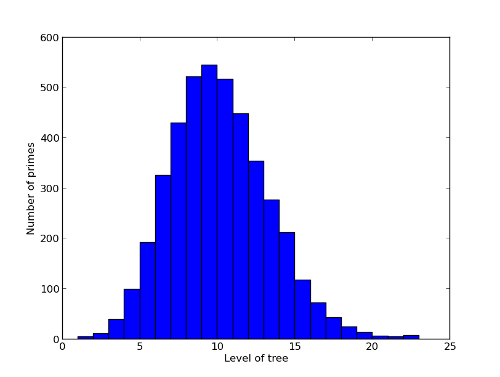
How bushy are these trees? The number of nodes at each level increases up to a maximum of 545 nodes at level 9 then decreases. The levels of the suffix primes in their respective trees is given in the histogram below.

Is it obvious that the number of suffix primes is finite? (Ie., it isn’t obvious to me.)
Ken: you can start with single digit primes and build the tree of suffix primes at the next level. When a number is composite for all digits you add to the front, that’s the end of that line. When you show that all lines end, you’re done. So while it’s not obvious, you can grind it out.
2 and 5 are out because of our non-prime base, which raises a couple of questions.
First, which bases are most diverse (non orphan trees/base)? Is there a maximum on SPs?
Second, which bases will have the greatest density of suffix primes (I.e. suffix primes/primes up to the highest sp?)
I assume prime bases are the answer for all these questions, but it’s non-obvious to this non-mathematician whether you’ll hit a maximum as base increases.
John: That’s good to see, I suppose “a big hairy mess” isn’t so surprising. I think the histogram to represent the data is also a good choice.
Ken: There could be an argument that these trees are always going to be finite using the prime number theorem which concerns the distribution of primes. If the tree were infinite this would supply too many primes contradicting the theorem.
Ken: Actually checking again, that argument doesn’t work to give a simple proof, sorry. However what I had in mind was to estimate the number of suffix series for a random set of numbers which are distributed with the same rough distribution as the primes, x / ln x. In this situation the probability of having a tree with n levels drops exponentially for n large. (I don’t consider this easy to see, and I suspect any number theorist would give a much better argument).
Cool visualization approach. Here’s a related conversation.
John: You are not including 107, and other primes prepending #0. I would contend that since 7 is prime, so is 07, which is the suffix of 107, which is also prime.
Craig: For bases of similar size (in the same order of (decimal) magnitude for example) I believe you are right in assuming that the prime bases would have the the most suffix primes. Mind you, this is a gut feeling, so I can’t prove it for you. Similarly, my gut feeling is that because of the distribution of primes, just as there is a order of magnitude that contains the most primes, there would be a base that contains the most suffix primes.