This morning Andrew Stacey posted a beautiful identity I’d never seen before relating the golden ratio ϕ and the imaginary unit i:
![]()
Here’s a proof:
By De Moivre’s formula,
![]()
and so
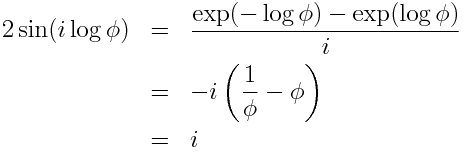
This morning Andrew Stacey posted a beautiful identity I’d never seen before relating the golden ratio ϕ and the imaginary unit i:
![]()
Here’s a proof:
By De Moivre’s formula,
![]()
and so
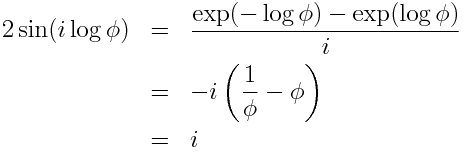
Comments are closed.
That’s just beautiful. Thanks.
Very neat.
I’d never heard of De Moivre’s before, and even after reading through the Wikipedia page, wondered why you reference it instead of simply referencing Euler’s identity, from which your second equality follows pretty naturally.
I don’t see why (1/phi – phi) should equal -1 ?
What have I missed here?
@Peter Fry
Phi is a solution to the equation x^2 – x – 1 = 0, so clearly 1 – phi^2 = -phi
Incredibly elegant. Thanks for sharing. This is amazing.
This is a beautiful identity.. I haven’t seen it before either.
There’s imaginary silver, too. If we introduce:
\phi_n = n + \frac{1}{\phi_n}
So that \phi_1 is the ordinary golden ratio, \phi_2 the “silver ratio”, etc, then:
2 \sin \imath \log \phi_n = n \imath