The previous post gave a relationship between the imaginary unit i and the golden ratio. This post highlights a comment to that post explaining that the relationship generalizes to generalizations of the golden ratio.
GlennF pointed out that taking the larger root of the equation
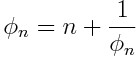
defines the golden ratio when n = 1, the silver ratio when n = 2, etc. φn is also the continued fraction made entirely of n‘s.
With this definition, we have
![]()

Did you see the cosine version? Then you get 2 cos(i log(psi_n)) = n, where psi_n is a root of x + 1/x = n. (It’s too late in the evening for me to work out the relationship between psi_n and phi_n.)
The relation between \phi_n and \psi_m only seems to be a nice one for some cases. For example \psi_3 = (1 + \phi_1), which is what the cosine relation on Andrew Stacey’s page uses. There are others, e.g. \psi_6 = 1 + 2 \phi_2.
I would like a ration of gold better than golden ratio, I think. (Sorry, belatedly pointing out the typo.)