Amazing approximation to e

Posted on by John

Here’s an approximation to e by Richard Sabey that uses the digits 1 through 9 and is accurate to over a septillion digits. (A septillion is 1024.)

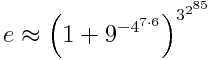
e \approx \left( 1 + 9^{{-4}^{7ḑot6}}\right)^{3^{2^{85}}}

MathWorld says that this approximation is accurate to 18457734525360901453873570 decimal digits. How could you get an idea whether this claim is correct? We could show that the approximation is near e by showing that its logarithm is near 1. That is, we want to show

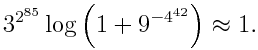
3^{2^{85}} \log \left( 1 + 9^{{-4}^{42}\right) \approx 1.

Define k to be 3^(2^85) and notice that k also equals 9^(4^42). From the power series for log(1 + x) and the fact that the series alternates, we have

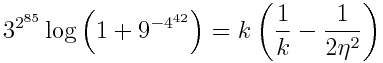
3^{2^{85}} \log \left( 1 + 9^{{-4}^{42}\right) = k \left( \frac{1}{k} - \frac{1}{2\eta^2} \right)

where η is some number between 0 and 1/k. This tells that the error is extremely small because 1/k is extremely small. It also tells us that the approximation underestimates e because its logarithm is slightly less than 1.

Just how small is 1/k? Its log base 10 is around −1.8 × 10^25, so it’s plausible that the approximation is accurate to 10^25 decimal digits. You could tighten this argument up a little and get the exact number of correct digits.

7 thoughts on “Amazing approximation to e”

  1. Leonid Boytsov

    Well, it is not exactly VERY surprising. (1+1/n)^n converges to e. In this case, you have an extremely large n = 3^(2^85)

  5. Phil

    John, do you mean that η (eta) should be a little bigger than k? That would make the second term small. If I’m following, then that error term would be something like 1/k–which means that the size of the error has a linear relation to the size of the input k. What would be really fun is some other approximation where this relation is a square or a cube.

  6. Joseph

    @vonjd For this specific result, probably. If you’re using it for numerics (except perhaps for arbitrary precision perhaps) you’re better off just loading a pre-defined bit pattern which is accurate to whatever precision you want. (And possibly also for arbitrary precision).

    For analytic purposes, you just keep e symbolic.

    However, the method of finding the number of digits something is valid to (though perhaps in bits instead of decimal) is more generally useful.

    IMHO. :)

  7. GlennF

    Even more amazing if you add (15-14)/(11+13-10-12) to the exponent (It will roughly double the number of digits)

Comments are closed.