Fibonacci formula for pi

Posted on by John

Here’s an unusual formula for pi based on the product and least common multiple of the first m Fibonacci numbers.

 

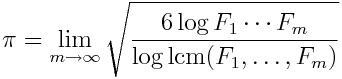
\pi = \lim_{m\to\infty} \sqrt{\frac{6 \log F_1 \cdots F_m}{\log \mbox{lcm}( F_1, \ldots, F_m )}}

Unlike the formula I wrote about a few days ago relating Fibonacci numbers and pi, this one is not as simple to prove. The numerator inside the root is easy enough to estimate asymptotically, but estimating the denominator depends on the distribution of primes.

Source: Yuri V. Matiyasevich and Richard K. Guy, A new formula for π, American Mathematical Monthly, Vol 93, No. 8 (October 1986), pp. 631-635.

 

3 thoughts on “Fibonacci formula for pi”

  1. Mike G.

    Fascinating… Another one of those “how would anyone even think of that?”

    Assuming I didn’t screw up my little Mathematica experiment, I don’t think this formula is ever going to be very popular. It does look like it converges (I didn’t really doubt that), but not very quickly…

    {
    {1000, 3.13672},
    {2000, 3.1388},
    {3000, 3.14007},
    {4000, 3.14062},
    {5000, 3.14057},
    {6000, 3.14091},
    {7000, 3.14097},
    {8000, 3.14096},
    {9000, 3.14115},
    {10000, 3.14117}
    }

  2. Jerome

    >> “how would anyone even think of that?”

    I guess the form presented here has been “solved for pi”. Originally, it probably stated:

    lim log(F_1…F_M) / log lcm(F_1, …, F_M) = π² / 6,

    in which π²/6 is the number also appearing as ζ(2), i.e. the sum of inverse squares.

    Since the least common multiple can be seen as being “equal to the product but with redundant prime factors removed”, this is just a statement about how many factors the Fibonacci numbers have in common. It can be interpreted very vaguely as “every ζ(2)th prime factor in the product F_1…F_M is redundant”. The number ζ(2) itself is related to prime numbers by

    ζ(2) = Π_p p² / (p² − 1),

    where the product is over all primes.

Comments are closed.