A Pythagorean triple is a list of positive integers (a, b, c) such that a2 + b2 = c2. Euclid knew how to find all Pythagorean triples: pick two positive integers m and n with m > n and let
a = m2 – n2, b = 2mn, c = m2 + n2.
Now what if we look at matrices with integer entries such that A2 + B2 = C2? Are there any? Yes, here’s an example:
![\left[ \begin{array}{rr} 11 & -12 \\ 4 & -3 \end{array} \right]^2 + \left[ \begin{array}{rr} 36 & -48 \\ 16 & -20 \end{array} \right]^2 = \left[ \begin{array}{rr} 37 & -48 \\ 16 & -19\end{array} \right]^2](http://www.johndcook.com/matrix_pythagorean_triple.png){kind=small}
How can you find matrix-valued Pythagorean triples? One way is to create diagonal matrices with Pythagorean triple integers. Take a list of n Pythagorean triples (ai, bi, ci) and create diagonal matrices A, B, and C with the ai along the diagonal of A, bi along the diagonal of B, and ci along the diagonal of C.
But that seems cheap. We’re really not using any properties of matrix multiplication other than the fact that you can square a diagonal matrix by squaring its elements. One way to create more interesting matrix Pythagorean triples is to start with the diagonal matrices described above and conjugate them by some matrix Q with integer entries such that Q-1 also has integer entries. Here’s why that works:
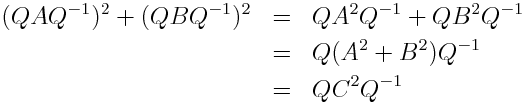
The example above was created by starting with the Pythagorean triples (3, 4, 5) and (5, 12, 13), creating diagonal matrices, and conjugating by
![Q = \left[ \begin{array}{rr} 3 & 2 \\ 2 & 1 \end{array} \right]](http://www.johndcook.com/qdef.png){kind=small}
This gives a way to create lots of matrix Pythagorean triples, but there may triples that this procedure leaves out.
Your procedure is equivalent to applying the conjugation idea to construct matrices m and n and then putting them into Euclid’s formulas. The standard way of checking that Euclid’s formulas give a Pythagorean triple works for matrices, but only if we assume the matrices m and n commute. This is why the same Q has to be used to form both.
The standard correspondence for positive real number is symmetric positive definite matrix. Here this means choosing positive integers for the diagonal matrices to construct m and n where the diagonal elements also have to satisfy the inequality. It may be interesting to allow zeros and symmetric positive semi-definite matrices.
Small typo in “Now what if we look at matrices with integer entries such that A^2 + B^2 = C?” — should be C^2, right?
Try to prove/disprove the matrix analogue of the Fermat’s Last theorem :)
so given integer pythagorean triplets, we can find infinitely many matrix pythagorean triplets.
now is there a reverse construction or relation?
It may be that for every matrix Pythagorean triple, the matrices A, B and C will commute (i.e., they will share a matrix of eigenvectors Q) and the corresponding eigenvalues will be standard Pythagorean triples.
Not all 2×2 matrix Pythagorean triples can be constructed as John describes. The following family of counterexamples is, regrettably, very boring. Take any matrix M, let (a,b,c) be an ordinary Pythagorean triple; then (aM)^2 + (bM)^2 = (cM)^2. This is true, in particular, even when M is not the result of conjugating a diagonal matrix with something in SL2(Z); for instance, take M = [1 1; 0 1] or, I think, [1 1; -1 1].
Here’s a marginally less boring sort-of-counterexample: take A = [1 0; 0 1] and B = [0 1; -1 0]; then A^2 + B^2 = 0 = 0^2. Perhaps that’s a cheaty counterexample because C is the zero matrix, in which case take C = [0 1; 0 0] instead.
Perhaps John’s construction yields all the possible *symmetric positive definite* matrix Pythagorean triples? I suspect not, but with little confidence.
It is an old thread, but I will post a reply.
There are non trivial cases.
For example,
If A = [30,13;3,0], B = [4,8;12,16], C = [-26,-25;-15,4].
then A^2 + B^2 = C^2.
A, B and C do not commute.
How can you generate a noncommutative matrices A, B and C that will satisfy that equation?
It is possible to generate such non commutative matrices of any n by n size. The result will appear in American Mathematical Monthly either this year (not likely) or early next year. The paper was accepted seven months ago, but they are backlogged.