Here are a couple elegant series involving the golden ratio φ = (1 + √5)/2.
First, reciprocals of integer powers:
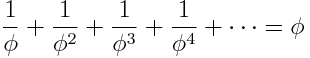
Then reciprocals of odd powers:
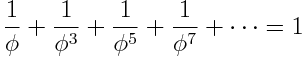
Both are easy to prove since they’re geometric series.
More posts related to the golden ratio:
Here are a couple elegant series involving the golden ratio φ = (1 + √5)/2.
First, reciprocals of integer powers:
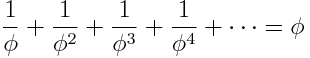
Then reciprocals of odd powers:
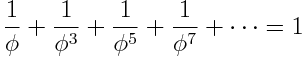
Both are easy to prove since they’re geometric series.
More posts related to the golden ratio:
Comments are closed.
It also then follows the sum of even powers of 1/phi (except for the zero power) is just 1/phi. Those three identities together are quite lovely.