There are four basic types of integral equations. There are many other integral equations, but if you are familiar with these four, you have a good overview of the classical theory.
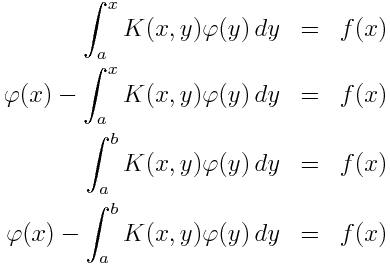
All four involve the unknown function φ(x) in an integral with a kernel K(x, y) and all have an input function f(x). In all four the integration ranges from some fixed lower limit. In the Volterra equations, the upper limit of integration is the variable x, while in the Fredholm equations, the upper limit of integration is a fixed constant.
The so-called equations of the first kind only involve the unknown function φ inside the integral. The equations of the second kind also involve φ outside the integral.
So the four equations above are
- Volterra equation of the first kind
- Volterra equation of the second kind
- Fredholm equation of the first kind
- Fredholm equation of the second kind
Here’s a diagram to make these easier to keep straight:
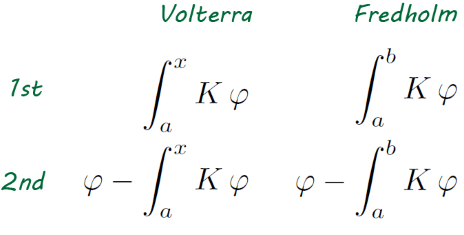
In general, the theory of Volterra equations is easier than that of Fredholm equations. And while equations of the first kind look simpler at first, it’s common to reduce equations of the first kind to equations of the second kind and concentrate on the later.
There are many variations on this theme. The x in Volterra equations could be a vector. The integral could be, for example, a double or triple integral. In Fredholm equations, the integration may be over fixed general region. Maybe you’re integrating over a watermelon, as the late William Guy would say. You could have nonlinear versions of these equations where instead of multiplying K(x, y) times φ(y) you have a kernel K(x, y, φ(y)) that is some nonlinear function of φ.
You may see references to Volterra or Fredholm equations of the third kind. These are an extension of the second kind, where a function A(x) multiples the φ outside the integral. Equations of the second kind are the most important since the first and third kinds can often be reduced to the second kind.
Related: Differential equation consulting

Survey article covering application areas for these four?
Theoretical survey article covering open questions for these?
Thanks for this.
I may write more about this in the future.
Excellent post. Could you please tell us about their application in physical sciences, if any? Thanks.
Do you know Martin Costabel. One of the best teachers I had, in this subject
No, I haven’t had the pleasure of meeting him.
what about equations of form
u(x,t)=int_{-inf}^{=inf} int _{0}^{t}k(x-y)(t-s)u(y,s)dsdy+f(x,t)
this seems integral equation in two variables.
volterra second type with respect to to t and Fredhom second type with respect to x.