Mathematical balance of trade

Areas of math all draw on and contribute to each other. But there’s a sort of trade imbalance between areas. Some, like analytic number theory, are net importers. Others, like topology, are net exporters.

Analytic number theory uses the tools of analysis, especially complex analysis, to prove theorems about integers. The first time you see this it’s quite a surprise. But then you might expect that since analysis contributes to number theory, then number theory must contribute to analysis. But it doesn’t much.

Topology imports ideas from algebra. But it exports more than in imports, to algebra and to other areas. Topology started as a generalization of geometry. Along the way it developed ideas that extend far beyond geometry. For example, computer science, which ostensibly has nothing to do with whether you can continuously deform one shape into another, uses ideas from category theory that were developed initially for topology.

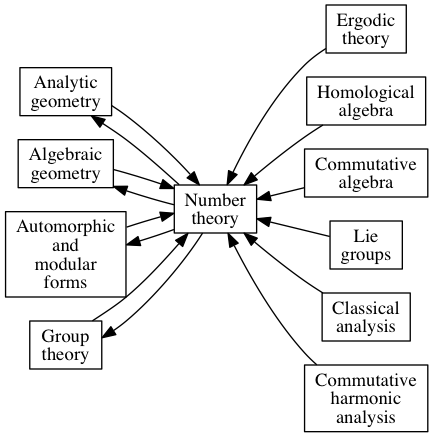
Here’s how Jean Dieudonné saw things. The following are my reconstructions of a couple diagrams from his book Panorama of Pure Mathematics, as seen by N. Bourbaki. An arrow from A to B means that A contributes to B, or B uses A.

For number theory, some of Dieudonné’s arrows go both ways, some only go into number theory. No arrows go only outward from number theory.

With topology, however, there’s a net flux out arrows going outward.

These diagrams are highly subjective. There’s plenty of room for disagreement. Dieudonné wrote his book 35 years ago, so you might argue that they were accurate at the time but need to be updated. In any case, the diagrams are interesting.

Update: See the next post of a larger diagram, sewing together little diagrams like the ones above.