Here’s a surprising result: The least common multiple of the first n positive integers is approximately exp(n).
More precisely, let φ(n) equal the log of the least common multiple of the numbers 1, 2, …, n. There are theorems that give upper and lower bounds on how far φ(n) can be from n. We won’t prove or even state these bounds here. See [1] for that. Instead, we’ll show empirically that φ(n) is approximately n.
Here’s some Python code to plot φ(n) over n. The ratio jumps up sharply after the first few values of n. In the plot below, we chop off the first 20 values of n.
from scipy import arange, empty
from sympy.core.numbers import ilcm
from sympy import log
import matplotlib.pyplot as plt
N = 5000
x = arange(N)
phi = empty(N)
M = 1
for n in range(1, N):
M = ilcm(n, M)
phi[n] = log(M)
a = 20
plt.plot(x[a:], phi[a:]/x[a:])
plt.xlabel("$n$")
plt.ylabel("$\phi(n) / n$")
plt.show()
Here’s the graph this produces.
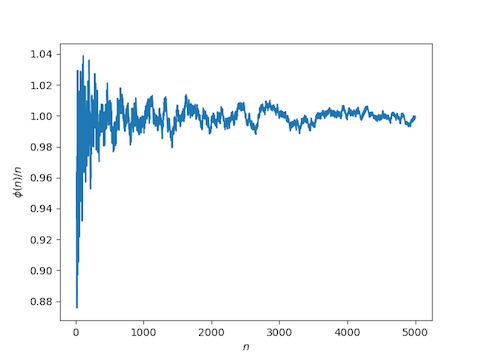
[1] J. Barkley Rosser and Lowell Schoenfeld. Approximate formulas for some functions of prime numbers. Illinois Journal of Mathematics, Volume 6, Issue 1 (1962), 64-94. (On Project Euclid)

Interesting to compare this with Stirling’s formula, as a measure of the asymptotic badness of $n!$ as a first guess or upper bound on $\text{lcm}(1:n)$.
Isn’t \phi(n) a bad choice of notation here, given Euler’s totient function?
Amazing tidbit of knowledge! (sorry for the content-less remark)
Very nice, indeed. I did not know that. But I am far from an expert in this kind of number theory.
For n=1000000000 we have phi(n)/n = 0.9999824279662022 (obviously by a method different from the method in the post).
@David Malone: Yes, it’s unfortunate notation, but it matches the paper I referenced.
In the paper you reference, phi(n) denotes the number of positive integers <= n and relatively prime to n.
In the paper, psi(n) is the logarithm of the least common multiple of all positive integers <= n.
It seems you are using the inequality
(1-epsilon)x< psi(x) e^5000.
Do you know if it tends to a limit?