Take a function that has a power series with a finite radius of convergence. Then the zeros of the partial sums will be dense around the boundary of convergence. That is Jentzsch’s theorem.
Here are a couple plots to visualize Jentzsch’s theorem using the plotting scheme described in this post.
First, we take the function f(z) = 1/(1 + z²). This function has singularities as i and −i, and so the radius of convergence is 1. These singularities correspond to the two white dots in the plot below.
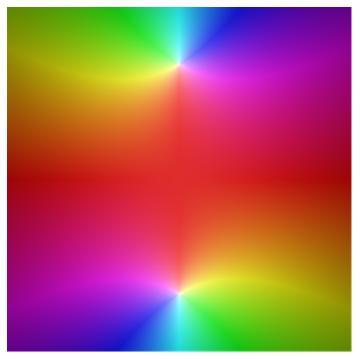
Now let’s look at the Taylor series for f.
f(z) = 1 − z2 + z4 − z6 + z8 − …
The series only converges inside the unit circle, but the partial sums are just polynomials and so are defined everywhere. Here we plot the partial sum up to z20.
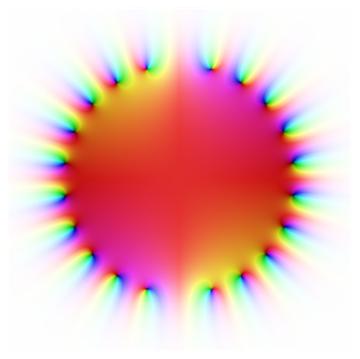
The black dots around the unit circle are zeros. The color quickly lightens as you move away from the unit circle because the function values grow quickly. Inside the unit circle, the two graphs match well, though of course outside they are very different.
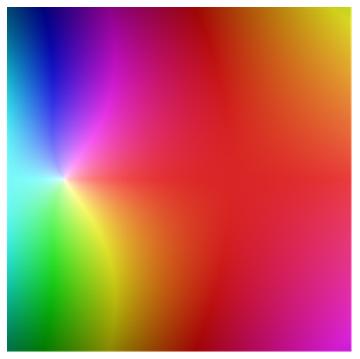
Here’s another example. This time we’ll look at the gamma function. The power series centered at 1 has radius 1 because the function has a pole at 0.
Here’s a plot of the gamma function. Note the white dot which is the singularity at 0.
And here’s a plot of the first 20 terms of the Taylor series centered at 1.
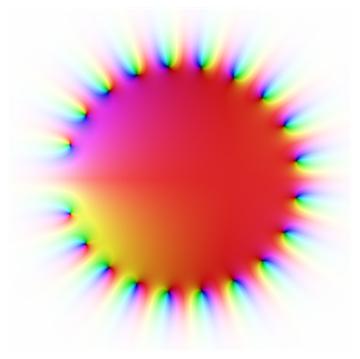

Wow! How come nobody every told me (or wikipedia apparently) about this extraordinary result? Do you have a reference for a nice proof?
I observe that, for any complex c, f(z)-c has a finite radius of convergence, so every point on the boundary will be an accumulation point of points for which a partial sum = c.