It occurred to me recently that I rarely hear about finite rings. I did a Google Ngram search to make sure this isn’t just my experience.
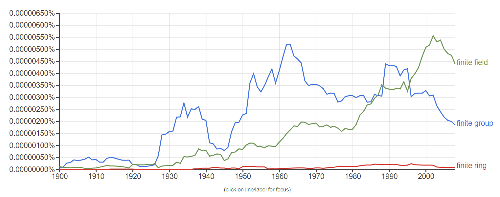
Why are finite groups and finite fields common while finite rings are not?
Finite groups have relatively weak algebraic structure, and demonstrate a lot of variety. Finite fields have very strong algebraic structure. Their complete classification has been known for a long time and is easy to state.
I imagine that most of the references to finite groups above have to do with classifying finite groups, and that most of the references to finite fields have to do with applications of finite fields, which are many.
You can see that references to finite groups hit their peak around the time of the Feit-Thompson theorem in 1962, and drop sharply after the classification of finite simple groups was essentially done in 1994. There’s a timeline of the progress toward the classification theorem on Wikipedia.
Rings have more structure than groups, but less structure than fields. Finite rings in particular are in a kind of delicate position: they easily become fields. Wedderburn’s little theorem says every finite domain is a field.
The classification of finite rings is much simpler than that of finite groups. And in applications you often want a finite field. Even if a finite ring (not necessarily a field) would do, you’d often use a finite field anyway.
In summary, my speculation as to why you don’t hear much about finite rings is that they’re not as interesting to classify as finite groups, and not as useful in application as finite fields.
Posts on finite simple groups
Posts on finite fields
- Brief introduction to finite fields
- Sum-product theorem for finite fields
- Encryption posts, many using finite fields

What do you mean when you say “The classification of finite rings is much simpler than that of finite groups”? Given any finite group G, you can construct, for example, the group ring G[Z_n] of formal linear combinations of elements of G with coefficients in Z_n, which contains G as a subgroup of its group of units.
@Nathan, all finite groups are subgroups of finite symmetric groups, yet most people would be happy to say that finite symmetric groups are classified, while finite groups are not.
@Gabriel: The difference is that embedding an arbitrary group in a symmetric group does not preserve any of its structure, whereas constructing the group ring does. Does anyone know if nonisomorphic groups can produce isomorphic group rings?
Actually, it’s virtually impossible to classify either finite rings or finite fields. In either case, nilpotence leads to vast wilderness of choices.
Finite simple rings are much easier to classify than finite simple groups.
@Nathan: over C this is not hard – any two groups with the same character degrees (with multiplicity) work. The smallest nonabelian example is the dihedral and quaternions groups of order 8. Over Z, this was an open problem for a long time, but a counterexample for integral group rings was found by Hertweck (Annals of Math, 2001).