Envelopes of epicycloids (pretty pictures!)

Imagine two ants crawling around a circle at different speeds and draw a line between the two ants at regular time intervals. The position of the two ants at time t are (cos pt, sin pt) and (cos qt, sin qt) where p and q are integers, p > q > 0, and t comes from dividing the interval [0, 2π] into an integer number of points.

These lines form an envelope, a set of tangent lines, around a curve in the middle known as an epicycloid.

I found this via [1]. An interesting tidbit from the paper is that the number of cusps in each epicycloid is

(p – q) / gcd(p, q).

Here are some examples.

p = 4, q = 3

p = 4, q = 1

p = 7, q = 3

p = 9, q = 4

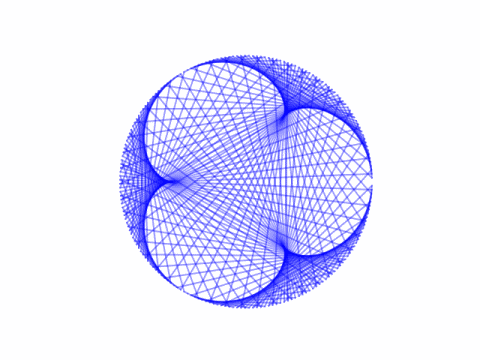
The equation of the epicycloid framed by the tangent lines is

$\begin{align*} x(\theta) =& \frac{p}{p+q} \cos\theta + \frac{q}{p+q} \cos \frac{p}{q}\theta \\ y(\theta) =& \frac{p}{p+q} \sin\theta + \frac{q}{p+q} \sin \frac{p}{q}\theta \\ \end{align*}$

Here’s the code that produced the plots above.

from numpy import sin, cos, linspace, pi
import matplotlib.pyplot as plt

def draw(p, q, n=200):
    xs = linspace(0, 2*pi, n)
    plt.axes().set_aspect(1)
    plt.axis('off')
    for x in xs:
        plt.plot([cos(p*x), cos(q*x)],
                 [sin(p*x), sin(q*x)], "b-", alpha=0.4)
    plt.show()
    plt.close()

draw(4, 3)
draw(4, 1)
draw(7, 3)
draw(9, 4)

If we let q be negative, we get hypocycloids instead. That’s the topic of the next post.

Related: Harmonographs

[1] Andrew Simoson. An Envelope for a Spirograph. The College Mathematics Journal, Vol. 28, No. 2 (Mar., 1997), pp. 134-139

2 thoughts on “Envelopes of epicycloids (pretty pictures!)”