There are only a few examples of Fourier series that are relatively easy to compute by hand, and so these examples are used repeatedly in introductions to Fourier series. Any introduction is likely to include a square wave or a triangle wave [1].
By square wave we mean the function that is 1 on [0, 1/2] and -1 on [1/2, 1], extended to be periodic.
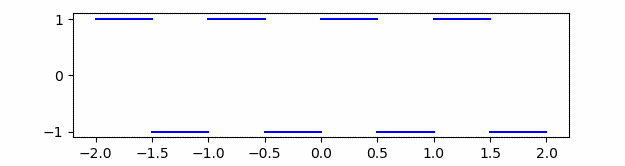
Its nth Fourier (sine) coefficient is 4/nπ for odd n and 0 otherwise.
By triangle wave we mean 1 – |2x – 1|, also extended to be periodic.
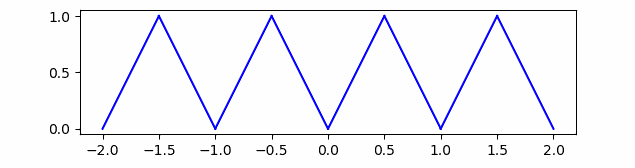
Its nth Fourier (cosine) coefficient is -4/(nπ)² for odd n and 0 otherwise.
This implies the Fourier coefficients for the square wave are O(1/n) and the Fourier coefficients for the triangle wave are O(1/n²). (If you’re unfamiliar with big-O notation, see these notes.)
In general, the smoother a function is, the faster its Fourier coefficients approach zero. For example, we have the following two theorems.
- If a function f has k continuous derivatives, then the Fourier coefficients are O(1/nk).
- If the Fourier coefficients of f are O(1/nk+1+ε) for some ε > 0 then f has k continuous derivatives.
There is a gap between the two theorems so they’re not converses.
If a function is continuous but not differentiable, the Fourier coefficients cannot decay any faster than 1/n², so the Fourier coefficients for the triangle wave decay as fast as they can for a non-differentiable function.
More post on rate of convergence
[1] The third canonical example is the saw tooth wave, the function f(x) = x copied repeatedly to make a periodic function. The function rises then falls off a cliff to start over. This discontinuity makes it like the square wave: its Fourier coefficients are O(1/n).

Who do you attribute these results to?
Intuitively, it takes substantial high-frequency components to make an abrupt change. So sharper changes means more high frequency contribution.
If you want to get more quantitative, every time you take a derivative of a Fourier series you pull out a factor of n. So the more derivatives the series has, the higher the power of n you can weight it by and the series still converge.
Heh. DLemire asked about “to who”, and you gave a very nice answer as “to what”. Which makes sense to me as I don’t think of you doing much history here.
Daniel, if you’re seriously curious about that, it sounds like a perfect question for https://hsm.stackexchange.com/, the math and science history StackExchange.
Thanks, Jonathan. I misread the question.
As for “who,” I expect it’s a long list of names. A lot of people made incremental process on various aspects of the convergence of Fourier series: Fourier, Poisson, Riemann, Lebesgue, etc.
Zygmund proved at least a special case of the theorems quoted above. He may have proved the general form. His book is the canonical reference on the topic.
How do the coefficients behave if f is smooth (or analytic)?
Since a smooth function is differentiable n times for any value of n, the coefficients have to go to zero faster than any polynomial.
You can see an example here where the coefficients approach zero exponentially fast.
Very well explained. Thank you for this