Fourier analysis

Fourier transform of a Fourier series

Posted on by John

The previous post showed how we can take the Fourier transform of functions that don’t have a Fourier transform in the classical sense.

The classical definition of the Fourier transform of a function f requires the integral of |f| over the real line to be finite. This implies f(x) must approach zero as x goes to ∞ and −∞. A constant function won’t do, and yet we got around that in the previous post. Distribution theory even lets you take the Fourier transform of functions that grow as their arguments go off to infinity, as long as they don’t grow too fast, i.e. like a polynomial but not like an exponential.

In this post we want to take the Fourier transform of functions like sine and cosine. If you read that sentence as saying Fourier series, you have the right instinct for classical analysis: you take the Fourier series of periodic functions, not the Fourier transform. But with distribution theory you can take the Fourier transform, unifying Fourier series and Fourier transforms.

For this post I’ll be defining the classical Fourier transform using the convention

{\cal F} \{ f(x) \}(\omega) = \hat{f}(\omega) = \int_{-\infty}^\infty \exp(-2\pi i \omega x)\, f(x)\, dx

and generalizing this definition to distributions as in the previous post.

With this convention, the Fourier transform of 1 is δ, and the Fourier transform of δ is 2π.

One can show that the Fourier transform of a cosine is a sum of delta functions, and the Fourier transform of a sine is a difference of delta functions.

\begin{align*} {\cal F} \{\cos 2\pi a x\} &= \frac{1}{2}\left(\delta(\omega - a) + \delta(\omega + a) \right) \\ {\cal F} \{\sin 2\pi a x\} &= \frac{1}{2i}\left(\delta(\omega - a) - \delta(\omega + a) \right) \end{align*}

It follows that the Fourier transform of a Fourier series is a sum of delta functions shifted by integers. In fact, if you convert the Fourier series to complex form, the coefficients of the deltas are exactly the Fourier series coefficients.

{\cal F}\left\{ \sum_{n=-\infty}^\infty c_n \exp(2\pi i n x) \right\} = \sum_{n=-\infty}^\infty c_n \delta(\omega - n)

Related posts

Fourier transform of a flat line

Posted on by John

Suppose you have a constant function f(x) = c. What is the Fourier transform of f?

We will show why the direct approach doesn’t work, give two hand-wavy approaches, and a rigorous definition.

Direct approach

Unfortunately there are multiple conventions for defining the Fourier transform.

For this post, we will define the Fourier transform of a function f to be

\hat{f}(\omega) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty \exp(-i \omega x)\, f(x)\, dx

If f(x) = c then the integral diverges unless c = 0.

Heuristic approach

The more concentrated a function is in the time domain, the more it spreads out in the frequency domain. And the more spread out a function is in the time domain, the more concentrated it is in the frequency domain. If you think this sounds like the Heisenberg uncertainty principle, you’re right: there is a connection.

A constant function is as spread out as possible, so it seems that its Fourier transform should be as concentrated as possible, i.e. a delta function. The delta function isn’t literally a function, but it can be made rigorous. More on that below.

Gaussian density approach

The Fourier transform of the Gaussian function exp(−x²/2) is the same function, i.e. the Gaussian function is a fixed point of the Fourier transform. More generally, the Fourier transform of the density function for a normal random variable with standard deviation σ is the density function for a normal random variable with standard deviation 1/σ.

As σ gets larger, the density becomes flatter. So we could think of our function f(x) = c as some multiple of a Gaussian density in the limit as σ goes to infinity. The Fourier transform is then some multiple of a Gaussian density with σ = 0, i.e. a point mass or delta function.

Rigorous approach

If f and φ are two well-behaved functions then

\int_{-\infty}^\infty \hat{f}(x) \, \varphi(x) \,dx = \int_{-\infty}^\infty f(x) \, \hat{\varphi}(x) \,dx

In other words, we can move the “hat” representing the Fourier transform from one function to the other. The equation above is a theorem when f and φ are nice functions. We can use it to motivate a definition when the function f is not so nice but the function φ is very nice. Specifically, we will assume φ is an infinitely differentiable function that goes to zero at infinity faster than any polynomial.

Given a Lebesgue integrable function f, we can think of f as a linear operator via the map

\varphi \mapsto \int_{-\infty}^\infty f(x) \, \varphi(x) \, dx

More generally, we can define a distribution to be any continuous [1] linear operator from the space of test functions to the complex numbers. A distribution that can be defined by integral as above is called a regular distribution. When we say we’re taking the Fourier transform of the constant function f(x) = c,  we’re actually taking the Fourier transform of the regular distribution associated with f. [2]

Not all distributions are regular. The delta “function” δ(x) is a distribution that acts on test functions by evaluating them at 0.

\delta: \varphi \mapsto \varphi(0)

We define the Fourier transform of (the regular distribution associated with) a function f to be the distribution whose action on a test function φ equals the integral of the product of f and the Fourier transform of φ. When a function is Lebesgue integrable, this definition matches the classical definition.

With this definition, we can calculate that the Fourier transform of a constant function c equals

\sqrt{2 \pi} \, c\, \delta

Note that with a different convention for defining the Fourier transform, you might get 2π c δ or just c δ.

An advantage of the convention that we’re using is that the Fourier transform of the Fourier transform of f(x) is f(−x) and not some multiple of f(−x). This implies that the Fourier transform of √2π δ is 1 and so the Fourier transform of δ is 1/√2π.

Related posts

[1] To define continuity we need to put a topology on the space of test functions. That’s too much for this post.

[2] The constant function doesn’t have a finite integral, but its product with a test function does because test functions decay rapidly. In fact, even the product of a polynomial with a test function is integrable

How Mathematica Draws a Dragonfly

Posted on by John

Mathematica includes code to draw various whimsical images. For example, if you enter the following command in Mathematica

    Entity["PopularCurve", "DragonflyCurve"][
        EntityProperty["PopularCurve", "Image"]]

you get an image of a dragonfly.

It draws such images with Fourier series. You can tell by asking for the parameterization of the curve. If you enter

    Entity["PopularCurve", "DragonflyCurve"][
        EntityProperty["PopularCurve", "ParametricEquations"]]

you’ll get the following, after some rearrangement.

    Function[t, {
        (7714/27) Sin[47/20 - t] + (1527/37) Sin[16/5 - 2t] + 
        (3202/39) Sin[108/41 - 3t] + … + 2/9 Sin[15/19 - 81 t], 
        (9406/37) Sin[29/7 - t] + (3591/53) Sin[28/13 - 2t] + 
        (1111/20) Sin[9/23 - 3t] + … -(3/29) Sin[8/23 + 81 t]
        }]

The function is a parameterized curve, taking t to (x(t), y(t)) where x(t) and y(t) are Fourier series including frequencies up to sin(81t). Each of the sine terms has a phase shift that could be eliminated by expressing sin(φ + ωt) as a linear combination of sin(ωt) and cos(ωt).

Presumably somebody drew the dragonfly, say in Adobe Illustrator or Inkscape, then did a Fourier transform of a sampling of the curve.

To make sure Mathematica wasn’t doing anything behind the scenes that I wasn’t aware of, I reproduced the dragonfly curve by porting the Mathematica code to Python.

The number of Fourier components needed to draw an image depends on the smoothness and complexity of the image. The curve for π, for example, the highest frequency component is sin(32t).

The triceratops curve is more complicated and Mathematica uses frequencies up to sin(188t).

 

Posthumous Chebyshev Polynomials

Posted on by John

Two families of orthogonal polynomials are named after Chebyshev because he explored their properties. These are prosaically named Chebyshev polynomials of the first and second kind.

I recently learned there are Chebyshev polynomials of the third and fourth kind as well. You might call these posthumous Chebyshev polynomials. They were not developed by Mr. Chebyshev, but they bear a family resemblance to the polynomials he did develop.

The four kinds of Chebyshev polynomials may be defined in order as follows.

\begin{align*} T_n(\cos\theta) &= \cos n\theta \\ U_n(\cos\theta) &= \frac{\sin (n+1)\theta}{\sin \theta} \\ V_n(\cos\theta) &= \frac{\cos \left(n+\frac{1}{2}\right)\theta}{\cos \frac{1}{2}\theta} \\ W_n(\cos\theta) &= \frac{\sin \left(n+\frac{1}{2}\right)\theta}{\sin \frac{1}{2}\theta} \\ \end{align*}

It’s not obvious that these definitions even make sense, but in each case the right hand side can be expanded into a sum of powers of cos θ, i.e. a polynomial in cos θ. [1]

All four kinds of Chebyshev polynomials satisfy the same recurrence relation

P_n(x) = 2x\,P_{n-1}(x) - P_{n-2}(x)

for n ≥ 2 and P0 = 1 but with different values of P1, namely x, 2x, 2x − 1, and 2x + 1 respectively [2].

Plots

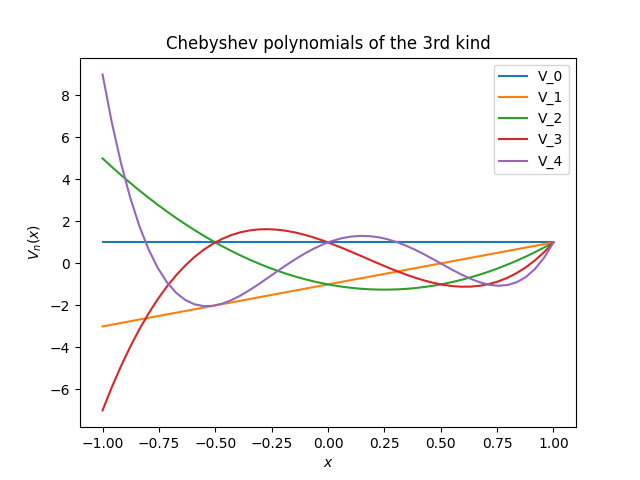
We can implement Chebyshev polynomials of the third kind using the recurrence relation above.

def V(n, x):
    if n == 0: return 1
    if n == 1: return 2*x - 1
    return 2*x*V(n-1, x) - V(n-2, x)

Here is a plot of Vn(x) for n = 0, 1, 2, 3, 4.

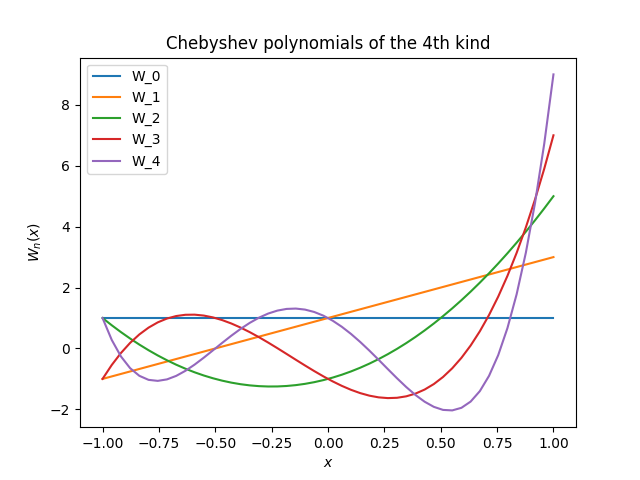
The code for implementing Chebyshev polynomials of the fourth kind is the same, except the middle line becomes

    if n == 1: return 2*x + 1

Here is the corresponding plot.

Square roots

The Chebyshev polynomials of the first and third kind, and polynomials of the second and fourth kind, are related as follows:

\begin{align*} V_n(x)&=\sqrt\frac{2}{1+x}T_{2n+1}\left(\sqrt\frac{x+1}{2}\right) \\ W_n(x)&=U_{2n}\left(\sqrt\frac{x+1}{2}\right) \end{align*}

To see that the expressions on the right hand side really are polynomials, note that Chebyshev polynomials of the first and second kinds are odd for odd orders and even for even orders [3]. This means that in the first equation, every term in T2n + 1 has a factor of √(1 + x) that is canceled out by the 1/√(1 + x) term up front. In the second equation, there are only even powers of the radical term so all the radicals go away.

You could take the pair of equations above as the definition of Chebyshev polynomials of the third and fourth kind, but the similarity between these polynomials and the original Chebyshev polynomials is more apparent in the definition above using sines and cosines.

The square roots hint at how these polynomials first came up in applications. According to [2], Chebyshev polynomials of the third and fourth kind

have been called “airfoil polynomials”, since they are appropriate for approximating the single square root singularities that occur at the sharp end of an airfoil.

Dirichlet kernel

There’s an interesting connection between Chebyshev polynomials of the fourth kind and Fourier series.

The right hand side of the definition of Wn is known in Fourier analysis as Dn, the Dirichlet kernel of order n.

D_n(\theta) = \frac{\sin \left(n+\frac{1}{2}\right)\theta}{\sin \frac{1}{2}\theta}

The nth order Fourier series approximation of f, i.e. the sum of terms −n through n in the Fourier series for f is the convolution of f with Dn, times 2π.

(D_n * f)(\theta) = 2\pi \sum_{k=-n}^n \hat{f}(k) \exp(ik\theta)

Note that Dn(θ) is a function of θ, not of x. The equation Wn(cos θ) = Dn(θ) defines Wn(x) where x = cos θ. To put it another way, Dn(θ) is not a polynomial, but it can be expanded into a polynomial in cos θ.

Related posts

[1] Each function on the right hand side is an even function, which implies it’s at least plausible that each can be written as powers of cos θ. In fact you can apply multiple angle trig identities to work out the polynomials in cos θ.

[2] J.C. Mason and G.H. Elliott. Near-minimax complex approximation by four kinds of Chebyshev polynomial expansion. Journal of Computational and Applied Mathematics 46 (1993) 291–300

[3] This is not true of Chebyshev polynomials of the third and fourth kind. To see this note that V1(x) = 2x − 1, and W1(x) = 2x + 1, neither of which is an odd function.

Trigonometric interpolation

Posted on by John

Suppose you want to interpolate a set of data points with a combination of sines and cosines.

One way to approach this problem would be to set up a system of equations for the coefficients of the sines and cosines. If you have N data points, you will get a system of N equations in N unknowns. The system will have a unique solution, though this is not obvious a priori.

Another approach would be to use the discrete Fourier transform (DFT). This is the approach that would commonly be used in practice. It’s even further from obvious a priori that this would work, but it does. (The DFT is so often computed using the FFT algorithm that the transform is often referred to by the algorithm name. If you’d like, mentally substitute FFT for DFT in the rest of the post.)

There are multiple ways to motivate the DFT, and the way suggested by the name is to derive the DFT as a discrete approximation to the (continuous) Fourier transform. Why should a discrete approximation to an integral transform also solve an interpolation problem? This doesn’t sound inevitable, or even plausible, but it is the case.

Another way to motivate the DFT is as the least-squares solution to fitting a sum of sines and cosines to a set of points. Since this is phrased as an optimization problem rather than an interpolation problem, it is clear that it will have a solution. However, it is not clear that the error in the optimal fit will in fact be zero. Furthermore, the equation for the coefficients in the solution is the same as the equation for the DFT. You can find a derivation in [1].

Example

Let’s take the vector [3, 1, 4, 1, 5, 9] and find trig functions that pass through these points. We can use the FFT as implemented in Python’s SciPy library to find a set of complex exponentials that pass through the points.

    from scipy.fft import fft
    from numpy import exp, array, pi, round

    x = array([3, 1, 4, 1, 5, 9])
    y = fft(x)

    N = len(x)
    z = [sum([exp(2j*pi*k*n/N)*y[k] for k in range(N)])/N for n in range(N)]

Aside from rounding errors on the order of 10−15 the vector z equals the vector x.

Turning the expression for z above into a mathematical expression, we have

f(z) = y0 + y1 exp(nπi/3) + y2 exp(2nπi/3) + y3 exp(nπi) + y4 exp(4nπi/3) + y5 exp(5nπi/3)

where the y‘s come from the FFT above.

To find sines and cosines we need to use Euler’s formula

exp(iθ) = cos(θ) + i sin(θ)

Because started with real data x, there will be symmetries in the FFT components x that simplify the reduction of the complex function f to a real-valued function g using sines and cosines; some of the components will be conjugate and so the complex parts cancel out.

6 g(x) = y0 + (y1 + y5) cos(πx/3) + (y2 + y4) cos(2πx/3) + y3 cos(πx)
+ i (y1 − y5) sin(πx/3) + (y2 − y4) cos(2πx/3)

and so

g(x) = 3.833 + 0.8333 cos(πx/3) − 1.833 cos(2πx/3) + 0.1666 cos(πx)
− 2.5981 sin(πx/3) − 2.0207 cos(2πx/3)

Here’s a plot that verifies that g(x) passes through the specified points.

Related posts

[1] William L. Briggs and Van Emden Henson. The DFT: An Owner’s Manual for the Discrete Fourier Transform. SIAM 1995.

Sawtooth waves

Posted on by John

I woke up around 3:00 this morning to some sort of alarm outside. It did not sound like a car alarm; it sounded like a sawtooth wave. The pattern was like a few Morse code O’s. Not SOS, or I would have gotten up to see if anyone needed help. Just O’s.

A sawtooth wave takes its name from the shape of its waveform: it looks like the edge of a saw. It also sounds a little jagged.

Sawtooth waves have come up several times here. For one thing, they have rich harmonics. Because the wave form is discontinuous, the Fourier coefficients decay to zero slowly. I wrote about that here. The post is about square waves and triangular waves, but sawtooth waves are very similar.

Here’s a post oscillators with a sawtooth forcing function.

I took sawtooth functions in a different direction in this post that started with an exercise from Knuth’s TAOCP. This led me down a rabbit hole on replicative functions and multiplication theorems in different contexts.

If I remember correctly the sound used for red alerts in Star Trek TOS started with a sawtooth wave. Early synthesizers had sawtooth generators because, as mentioned above, these waves are rich in overtones and can be manipulated to create interesting sounds such as the red alert sound.

The Clausen function

Posted on by John

I ran across the Clausen function the other day, and when I saw a plot of the function my first thought was that it looks sorta like a sawtooth wave.

Plot of Clausen function Cl_2

I wondered whether it also sounds like a sawtooth wave. More on that shortly.

The Clausen function can be defined in terms of its Fourier series:

\text{Cl}_2(x) = \sum_{k=1}^\infty \frac{\sin(kx)}{k^2}

The function commonly known as the Clausen function is one of a family of functions, hence the subscript 2. The Clausen functions for all non-negative integers n are defined by replacing 2 with n on both sides of the defining equation.

The Fourier coefficients decay quadratically, as do those of a triangle wave or sawtooth wave, as discussed here. This implies the function Cl2(x) cannot have a continuous derivative. In fact, the derivative of Cl2(x) is infinite at 0. This follows quickly from the integral representation of the function.

\text{Cl}_2(x)=-\int_0^x\log \left|2\sin\frac{t}{2} \right|\, dt

The fundamental theorem of calculus shows that the derivative

\text{Cl}'_2(x)=-\log \left|2\sin\frac{x}{2} \right|

blows up at 0.

How does it sound?

What does it sound like if we create music with Clausen waves rather than sine waves? I initially thought it sounded harsh, but that turned out to be an artifact of how I’d make the audio file. A reader emailed me a better recording using the first few notes of a famous hymn. It’s a much more pleasant sound than I had expected.

ein_feste_burg.wav

 

Related posts

Connecting the FFT and quadratic reciprocity

Posted on by John

Some readers will look at the title of this post and think “Ah yes, the FFT. I use it all the time. But what is this quadratic reciprocity?”

Others will look at the same title and think “Gauss called the quadratic reciprocity theorem the jewel in the crown of mathematics. But what is this FFT thing? I think I remember an engineer saying something about that.”

Gauss proved a theorem that relates quadratic reciprocity and the FFT. For distinct odd primes p and q, the following equation holds.

\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = \frac{\text{Tr} {\cal F}_{pq}}{ \text{Tr} {\cal F}_p\, \text{Tr} {\cal F}_q}

I’ll spend the rest of this post unpacking this equation.

Legendre symbols

The expressions on the left are not fractions but rather Legendre symbols. The parentheses are not for grouping but are part of the symbol.

The Legendre symbol

\left(\frac{a}{r}\right)

is defined to be 0 if a is a multiple of r, 1 if a has a square root mod r, and −1 otherwise.

Fourier transforms

The Discrete Fourier Transform (DFT) of a vector of length n multiplies the vector by the n by n Fourier matrix Fp whose j, k entry is equal to exp(2πi jk / n). The Fast Fourier Transform (FFT) is a way to compute the DFT more quickly than directly multiplying by the Fourier matrix. Since the DFT is nearly always computed using the FFT algorithm, the DFT is commonly referred to as the FFT.

Matrix trace

The trace of a matrix is the sum of the elements along the main diagonal. So the trace of the Fourier matrix of size n is

\text{Tr} {\cal F}_n = \sum_{j=1}^n \exp(2\pi ij^2/n)

Numerical illustration

The quadratic reciprocity theorem, also due to Gauss, is usually stated as

\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2}\frac{q-1}{2}}

We can illustrate the theorem at the top of the page numerically with the following Python code, using the quadratic reciprocity theorem to evaluate the product of the Legendre symbols.

from numpy import exp, pi

tr = lambda p: sum(exp(2j*pi*k**2/p) for k in range(1, p+1))
p, q = 59, 17
print( tr(p*q)/(tr(p)*tr(q)) )
print( (-1)**((p-1)*(q-1)/4) )

The first print statement produces (0.9999999999998136-1.4048176871018313e-13j) due to some loss of precision due to floating point calculations, but this is essentially 1, which is what the second print statement produces.

If we change q to 19, both statements print −1 (after rounding the first result).

Quadratic Gauss sum

We can quickly prove

\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = \frac{\text{Tr} {\cal F}_{pq}}{ \text{Tr} {\cal F}_p\, \text{Tr} {\cal F}_q}

if we assume the quadratic reciprocity theorem and the following equation for the trace of the Fourier matrix.

\text{Tr} {\cal F}_n = \sum_{j=1}^n \exp(2\pi ij^2/n) = \left\{ \begin{array}{ll} \sqrt{n} & \mbox{if } n \equiv 1 \bmod{4} \\ 0 & \mbox{if } n \equiv 2 \bmod{4} \\ i\sqrt{n} & \mbox{if } n \equiv 3 \bmod{4} \\ (1+i)\sqrt{n} & \mbox{if } n \equiv 0 \bmod{4} \\ \end{array} \right.

This proof is historically backward. It assumes quadratic reciprocity, but Gauss proved quadratic reciprocity by first proving the equation we’re trying to prove. He then obtained the expression on the right hand side of the quadratic reciprocity theorem using the equation above for the trace of the Fourier matrix.

The trace of the Fourier matrix is now called a quadratic Gauss sum. It’s a special case of more general sums that Gauss studied, motivated by his exploration of quadratic reciprocity.

Incidentally, Gauss gave many proofs of the quadratic reciprocity theorem. I don’t know where the proof outlined hear fits into the sequence of proofs he developed.

Related posts

Eigenvectors of the DFT matrix

Posted on by John

When is the discrete Fourier transform of a vector proportional to the original vector? And when that happens, what is the proportionality constant?

In more formal language, what can we say about the eigenvectors and eigenvalues of the DFT matrix?

Setup

I mentioned in the previous post that Mathematica’s default convention for defining the DFT has mathematical advantages. One of these is that it makes the DFT an isometry, that is, taking the DFT of a vector does not change its norm. We will use Mathematica’s convention here because that will simplify the discussion. Under this convention, the DFT matrix of size N is the square matrix whose (j, k) entry is

ωjk / √N

where ω = exp(-2π i/N) and the indices j and k run from 0 to N − 1.

Eigenvalues

Using the definition above, if you take the discrete Fourier transform of a vector four times, you end up back where you started. With other conventions, taking the DFT four times takes you to a vector that is proportional to the original vector, but not the same.

It’s easy to see what the eigenvalues of the DFT are. If transforming a vector multiplies it by λ, then λ4 = 1. So λ = ±1 or ±i. This answers the second question at the top of the post: if the DFT of a vector is proportional to the original vector, the proportionality constant must be a fourth root of 1.

Eigenvectors

The eigenvectors of the DFT, however, are not nearly so simple.

Suppose N = 4k for some k > 1 (which it nearly always is in practice). I would expect by symmetry that the eigenspaces of 1, −1, i and −i would each have dimension k, but that’s not quite right.

In [1] the authors proved that the eigenspaces associated with 1, −1, i and −i have dimension k+1, k, k−1, and k respectively.

This seems strange to me in two ways. First, I’d expect all the spaces to have the same dimension. Second, if the spaces did not have the same dimension, I’d expect 1 and −1 to differ, not i and −i. Usually when you see i and −i together like this, they’re symmetric. But the span of the eigenvectors associated with i has dimension one less than the dimension of the span of the eigenvectors associated with −i. I don’t see why this should be. I’ve downloaded [1] but haven’t read it yet.

[1] J. H. McClellan; T. W. Parks (1972). “Eigenvalues and eigenvectors of the discrete Fourier transformation”. IEEE Transactions on Audio and Electroacoustics. 20 (1): 66–74.

DFT conventions: NumPy vs Mathematica

Posted on by John

Just as there are multiple conventions for defining the Fourier transform, there are multiple conventions for defining the discrete Fourier transform (DFT), better known as the fast Fourier transform (FFT). [1]

This post will look at two DFT conventions, one used in Python’s NumPy library, and one used in Mathematica. There are more conventions in use, but this post will just look at these two.

In some sense the differences between conventions are trivial, but trivial doesn’t mean unimportant [1]. If you don’t know that there are multiple conventions, you could be quite puzzled when the output of a FFT doesn’t match your expectations.

NumPy definition

NumPy’s fft and related functions define the discrete Fourier transform of a sequence a0, a1, …, aN−1 to be the sequence A0, A1, …, AN−1 given by

A_k = \sum_{m=0}^{N-1} a_m \exp(-2\pi i mk/N)

Mathematica definition

Mathematica’s Fourier function defines the discrete Fourier transform of a sequence u1, u2, …, uN to be the sequence v1, v2, …, vN given by

v_k = \frac{1}{\sqrt{N}} \sum_{m=1}^{N} u_m \exp\big(-2\pi i (m-1)(k-1)/N\big)

This is the default definition in Mathematica, but not the only possibility. More on that below in the discussion of compatibility.

Motivation

Python arrays are indexed from 0 while Mathematica arrays are indexed starting from 1. This is why the inputs and outputs are numbered as they are.

Subtracting 1 from the m and k indices makes the two definitions visually less similar, but the terms in the two summations are the same. The only difference between the two implementations is the scaling factor in front of the sum.

Why does Mathematica divide the sum by √N while NumPy does not? As is often the case when there are differing conventions for defining the same thing, the differences are a result of which theorems you want to simplify. Mathematica complicates the definition of the DFT slightly, but in exchange makes the DFT and its inverse more symmetric.

The choice of scaling factor is consistent with the user bases of the two languages. Python skews more toward engineering and applied math, while Mathematica skews more toward pure math. In light of this, the choices made by Python and Mathematica seem inevitable.

Compatibility

Like Mathematica’s continuous Fourier transform function FourierTransform, its discrete Fourier transform function Fourier takes an optional FourierParameters argument for compatibility with other conventions. Setting the a parameter to 1 eliminates the √N term and produces a result consistent with NumPy.

There are more variations in DFT definitions. For example, some definitions of the DFT do not have a negative sign inside the exponential. Mathematica can accommodate this by setting b to −1 in thel FourierParameters argument. There are other possibilities too. In some implementations, for example, the 0 frequency DC term is in the middle rather than at the beginning.

[1] The FFT is an algorithm for computing the DFT, but the transform itself is often called the FFT.

[2] In classical education, the trivium consisted of grammar, logic, and rhetoric. The original meaning of “trivial” is closer to “foundational” than to “insignificant.”