In a comment to my previous post on quatrefoils, Jan Van lint suggested a different equation for quatrefoils:
r = a + |cos(2θ)|
Here are some examples of how these curves look for varying values of a.
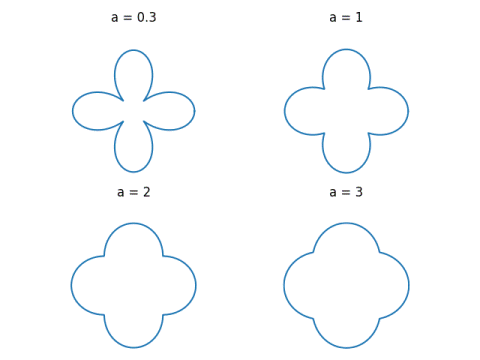
As a increases, the curves get rounder. We can quantify this by looking at the angle between the tangents on either side of the cusps. By symmetry, we can pick any one of the four cusps, so we’ll work with the one at θ = π/4 for convenience.
The slopes of the tangent lines are the left and right derivatives
Now the derivative of
a + |cos(2θ)|
with respect to θ at θ = π/4 is 2 from one size and -2 from the other.
Sine and cosine are equal at π/4, they cancel out in the ratio above and so the two derivatives, the slopes of the two tangent lines, are (2+a)/(2-a) and (2-a)/(2+a). The slopes are reciprocals of each other, which is what we’d expect since the quatrefoils are symmetric about the line θ = π/4.
The angles of the two tangent lines are the inverse tangents of the slopes, and so the angle between the two tangent lines is
Note that as a goes to zero, so does the angle between the tangent lines.
Here’s a plot of the angle as a function of a.
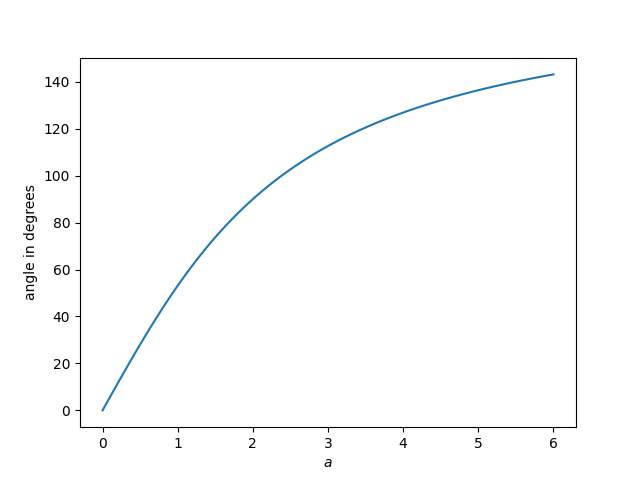
You could start with a desired angle and solve the equation above numerically for the value of a that gives the angle. From the graph above, it looks like if we wanted the curves to intersect at 90° we should pick a around 2. In fact, we should pick a exactly equal to 2. There the slopes are (2+2)/(2-2) = ∞ and (2-2)/(2+2) = 0, i.e. one tangent line is perfectly vertical and the other is perfectly horizontal.

Very nice analysis.
The area has a fairly nice formula: pi*a^2 + 4*a + pi/2. As the parameter a gets larger, the area goes to pi*a^2, which makes sense since the curve approaches a circle.
The label on the y axis should be degrees, not radians.