Counting triangles with integer sides

Let T(N) be the number of distinct (non-congruent) triangles with integer sides and perimeter N.  For example, T(12) = 3 because there are three distinct triangles with integer sides and perimeter 12. There’s the equilateral triangle with sides 4 : 4 : 4, and the Pythagorean triangle 3 : 4 : 5. With a little more work we can find 2 : 5 : 5.

The authors in [1] developed an algorithm for finding T(N). The following Python code is a direct implementation of that algorithm.

    def T(N :int):
        if N < 3:
            return 0
        base_cases = {4:0, 6:1, 8:1, 10:2, 12:3, 14:4}
        if N in base_cases:
            return base_cases[N]
        if N % 2 == 0:
            R = N % 12
            if R < 4:
                R += 12
            return (N**2 - R**2)//48 + T(R)
        if N % 2 == 1:
            return T(N+3)

If you’re running a version of Python that doesn’t support type hinting, just delete the :int in the function signature.

Since this is a recursive algorithm, we should convince ourselves that it terminates. In the branch for even N, the number R is an even number between 4 and 14 inclusive, and so it’s in the base_cases dictionary.

In the odd branch, we recurse on N+3, which is a little unusual since typically recursive functions decrease their argument. But since N is odd, N+3 is even, and we’ve already shown that the even branch terminates.

The code (N**2 - R**2)//48 raises a couple questions. Is the numerator divisible by 48? And if so, why specify integer division (//) rather than simply division (/)?

First, the numerator is indeed divisible by 48. N is congruent to R mod 12 by construction, and so N – M is divisible by 12. Furthermore,

N² – R² = (N – R)(N + R).

The first term on the right is divisible by 12, so if the second term is divisible by 4, the product is divisible by 48.  Since N and R are congruent mod 12, N + R is congruent to 2R mod 12, and since R is even, 2R is a multiple of 4 mod 12. That makes it a multiple of 4 since 12 is a multiple of 4.

So if (N² – R²)/48 is an integer, why did I write Python code that implies that I’m taking the integer part of the result? Because otherwise the code would sometimes return a floating point value. For example, T(13) would return 5.0 rather than 5.

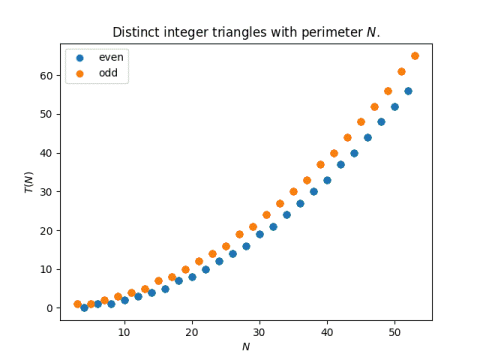
Here’s a plot of T(N).

[1] J. H. Jordan, Ray Walch and R. J. Wisner. Triangles with Integer Sides. The American Mathematical Monthly, Vol. 86, No. 8 (Oct., 1979), pp. 686-689