Some mathematical art

Posted on by John

This evening I ran across a paper on an unusual coordinate system that creates interesting graphs based from simple functions. It’s called “circular coordinates,” but this doesn’t mean polar coordinates; it’s more complicated than that. [1]

Here’s a plot reproduced from [1], with some color added (the default colors matplotlib uses for multiple plots).

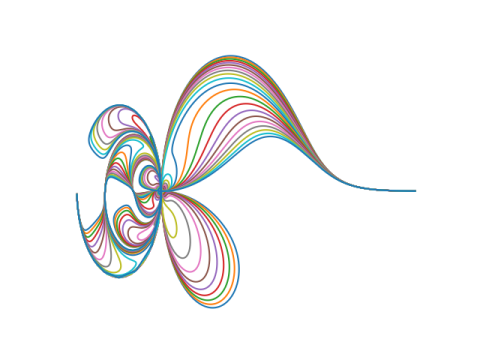
The plot above was based on a the gamma function. Here are a few plots replacing the gamma function with another function.

Here’s x/sin(x):

Here’s x5:

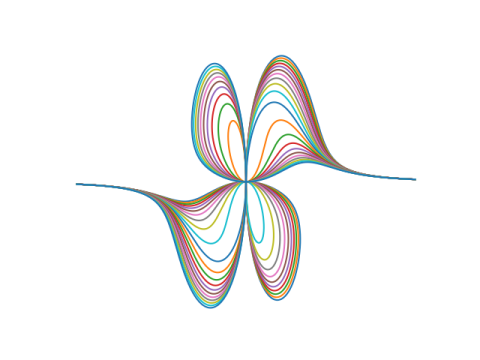
And here’s tan(x):

Here’s how the plots were created. For a given function f, plot the parametric curves given by

\begin{align*} x(t) &= \frac{2t \left(f(t) \right )^2}{t^2 + \left(f(t) \right )^2} \\ y(t) &= \frac{2t^2 f(t)}{t^2 + \left(f(t) \right )^2} \\ \end{align*}

See [1] for what this has to do with circles and coordinates.

The plots based on a function g(x) are given by setting f(x) = g(x) + c where c = −10, −9, −8, …, 10.

Related posts

[1] Elliot Tanis and Lee Kuivinen, Circular Coordinates and Computer Drawn Designs. Mathematics Magazine. Vol 52 No 3. May, 1979.

2 thoughts on “Some mathematical art”

  1. Ravi

    Is there a typo in your post, or have I misunderstood the maths?

    You say at teh end of the post

    “The plots based on a function g(x) are given by setting f(x) = g(x) + c…”

    Should that not be “f(x) = g(x) * c” – ie it is times c, not plus c

    Or have I got the maths wrong?

    PS I’m trying to play around with this in R

Comments are closed.