Start with a unit circle and draw the largest square you can inside the circle and the smallest square you can outside the circle. In geometry lingo these are the inscribed and circumscribed squares.
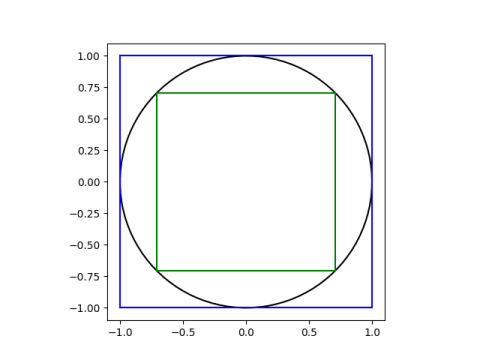
The circle fits inside the square better than the square fits inside the circle. That is, the ratio of the area of the circle to the area of the circumscribed square is larger than the ratio of the area of the inscribed square to the area of the circle.
David Singmaster [1] generalized this theorem to higher dimensions as follows:
The n-ball fits better in the n-cube than the n-cube fits in the n-ball if and only if n ≤ 8.
Singmaster rigorously proves his statement in his paper. Here I will illustrate that it’s true with a graph.
We need three facts. First, the volume of a ball in n dimensions is
rn πn/2 / Γ((n+2)/2).
Second, the volume of a cube in n dimensions with edge 2r is
(2r)n.
And finally, the edge of the inscribed cube is 2/√n. (To see this is right, note that the distance from the center of the cube to a corner is 1.)
This gives us all we need to create the following plot.
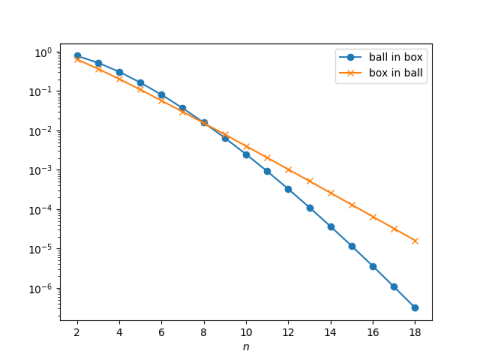
Both ratio curves go to zero quickly as n increases. (Note that the vertical scale is logarithmic, so the curves are going to zero exponentially.) This result is surprising but well known. Singmaster’s theorem about the ratio of the two curves is not as well known.
More high-dim geometry posts
[1] David Singmaster. On Round Pegs in Square Holes and Square Pegs in Round Holes. Mathematics Magazine, Nov., 1964, Vol. 37, No. 5, pp. 335-337

So if I’m shipping someone a garden-variety 3-D beach ball, it’s a better fit if I put the ball inside a box, than if I put a box inside the beach ball. That’s handy, in a Texas Aggie kind of way.