Carbon nanotube-like plots

A few days ago I wrote a brief post showing an interesting pattern that comes from plotting sin(1), sin(2), sin(3), etc.

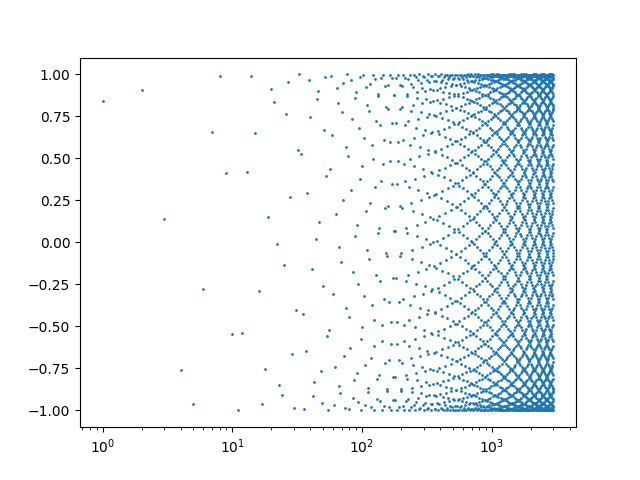
That post uses a logarithmic scale on the horizontal axis. You get a different, but also interesting, pattern when you use a linear scale.

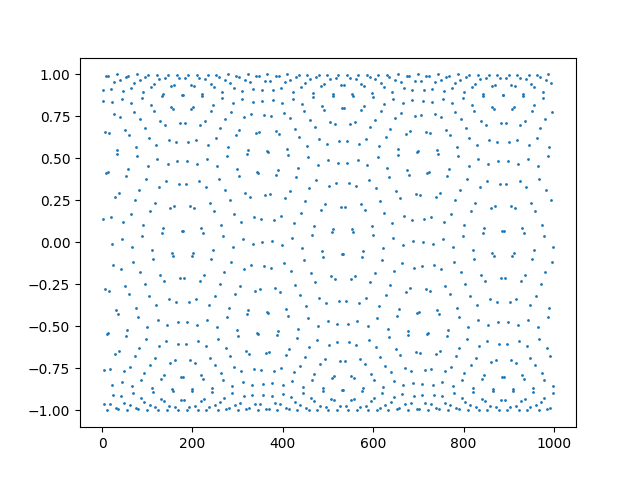
Someone commented that this looks like a projection of a carbon nanotube, and I think they’re right.

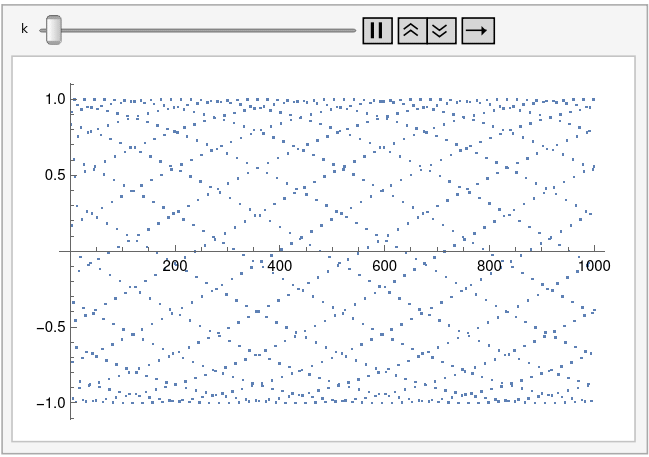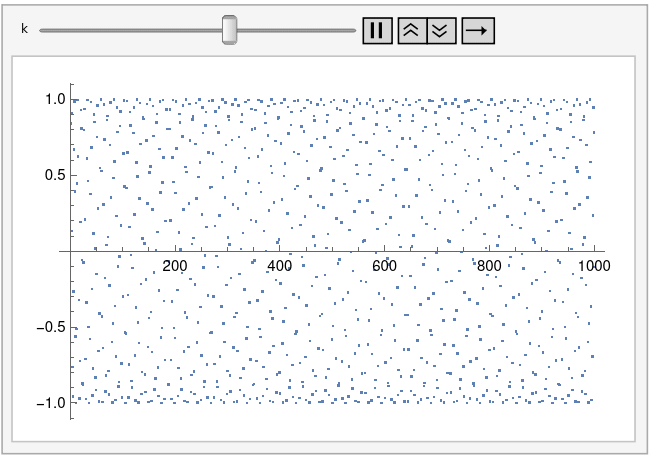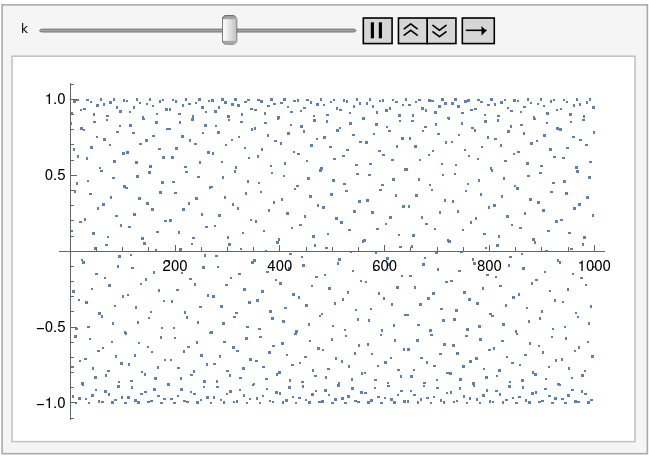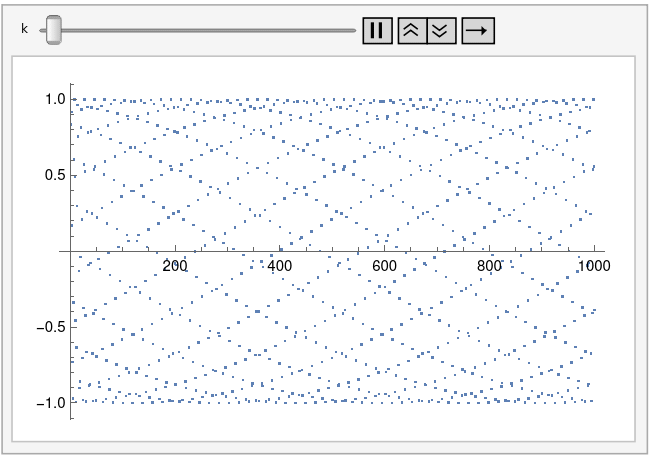
Let’s generalize this by plotting sin(kn) for integer n. The plot above corresponds to k = 1. Tiny changes to k make a big difference in the appearance of the plot.

Here’s k = 0.995:

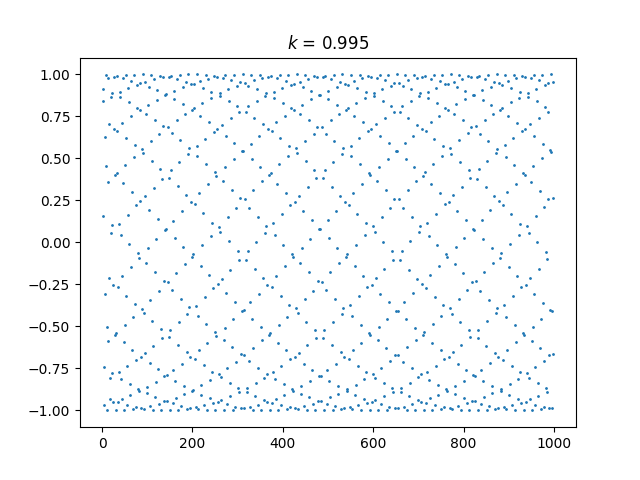
And here’s k = 1.005:

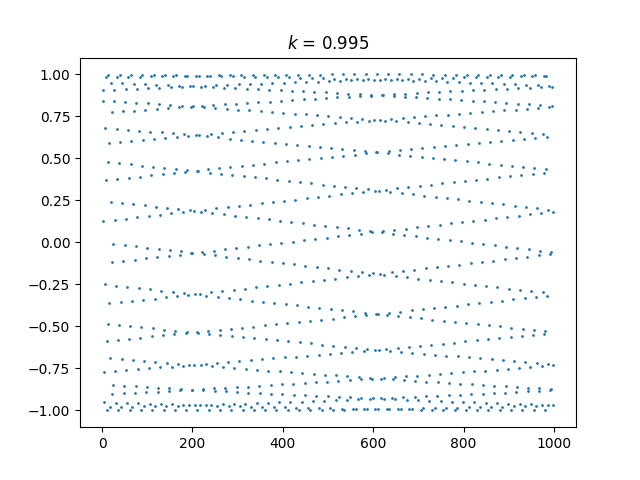
And here’s an animated plot, continuously changing k from 0.99 to 1.01.

This animation was created using the following Mathematica code.

    Animate[ListPlot[Table[Sin[k n], {n, 1, 1000}]], {k, 0.99, 1.01}, 
            AnimationRate -> 0.001, TrackedSymbols :> {k}]