Mental math trick and deeper issues

I’d like to do two things in this post. I’ll present a fun bit of mental math, then use it to illustrate a few deeper points.

The story starts with a Twitter thread I wrote on @AlgebraFact.

The Strait of Gibraltar is 13 km wide. How wide is that in miles?

You can convert km to miles with the ratio any two consecutive Fibonacci numbers.

8 and 13 are consecutive Fibonacci numbers, and 8/13 is convenient here.

So the Strait of Gibraltar is about 8 miles wide.

— Algebra Etc. (@AlgebraFact) January 28, 2022

The Fibonacci series begins

1, 1, 2, 3, 5, 8, 13, 21, ….

So this gives us a sequence of possible conversion factors:

1/1, 1/2, 2/3, 3/5, 5/8, 8/13, 13/21, ….

Which conversion factor is best?

“Best” depends on one’s optimization criteria. A lot of misunderstandings boil down to implicitly assuming everyone has the same optimization criteria in mind when they do not.

For the purposes of mentally approximating the width of the Strait of Gibraltar, 8/13 is ideal because the resulting arithmetic is trivial. Accuracy is not an issue here: surely the Strait is not exactly 13 kilometers wide. There’s probably more error in the 13 km statement than there is in the conversion to miles.

But what if accuracy were an issue?

The reason consecutive Fibonacci ratios make good conversion factors between miles and kilometers is that

F_n+1 / F_n → φ = 1.6180 …

as n grows, where φ is the golden ratio. We’re wanting to convert from kilometers to miles, so we actually want the conjugate golden ratio

1/φ = φ – 1 = 0.6180 …

This is very close to the number of miles in a kilometer, which is 0.6214.

So back to our question: which conversion factor is best, if by best we mean most accurate?

The further out we go in the Fibonacci sequence, the closer the ratio of consecutive numbers is to the golden ratio, so we should go out as far as possible.

Except that’s wrong. We’ve committed a common error: optimizing a proxy. We don’t want to get as close as possible to the golden ratio; we want to get as close as possible to the conversion factor. The golden ratio was a proxy.

Initially, getting closer to our proxy got us closer to our actual goal. As we progress through the sequence

1/1, 1/2, 2/3, 3/5, 5/8, 8/13, 13/21

we get closer to 1/φ = 0.6180 and closer to our conversion factor 0.6214. But after 13/21 our goals diverge. Going further brings us closer to 1/φ but further from our conversion factor as the following plot illustrates.

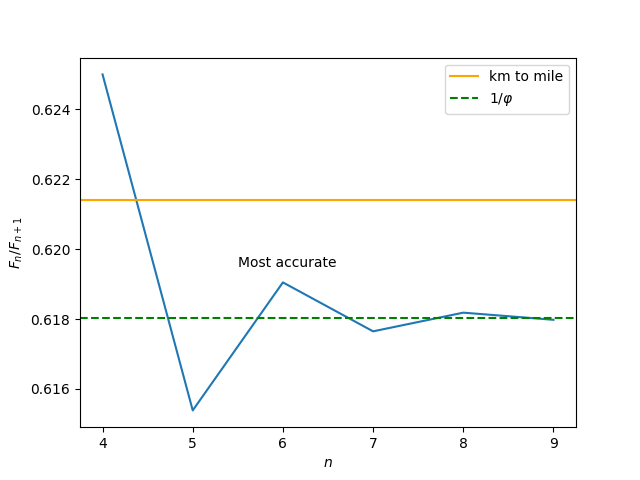
Optimizing a proxy is not an error per se, but reification is. This is when you lose sight of your goal and forget that a proxy is a proxy. Optimizing a proxy is a practical expedient, and may be sufficient, but you have to remain aware that that’s what you’re doing.

For more along these lines, see the McNamara fallacy.