Conditions for when solutions to an ODE will oscillate

Consider the second order linear differential equation

You could think of y as giving the height of a mass attached to a spring at time t where k is the stiffness of the spring. The solutions are sines and cosines with frequency √k. Think about how the solution depends on the spring constant k. If k is decreases, corresponding to softening the spring, the frequency of the solutions is decreases, and the period between oscillations increases.

Now suppose we replace the constant k with a decreasing positive function q(t). It seems that by controlling the decay rate of q we could control the oscillations of our system. For q decaying slowly but not too slowly, the solutions would continue to oscillate, crossing back and forth across the zero position, but with increasing time between crossings.

Below some critical rate of decay, the solutions may stop crossing the x axis at all. It seems plausible that if q decreases quickly enough, the period could decrease along with it at just the right rate so that the next oscillation never fully arrives.

Adolf Kneser (1862–1930) proved that the intuition described above is indeed correct. He proved that if

$\limsup _{t \to \infty} t^2 q(t) < \frac{1}{4}$

the solutions to

will eventually stop oscillating, but if

$\liminf _{t \to \infty} t^2 q(t) > \frac{1}{4}$

they will oscillate forever.

Example

We’ll set for initial conditions y(0) = 1 and y ‘(0) = 0.

Let q(t) = (1 + 0.1 t)^-1.9. This choice of q decays slower than 0.25 t^-2 and so our solutions should oscillate indefinitely. And that appears to be the case:

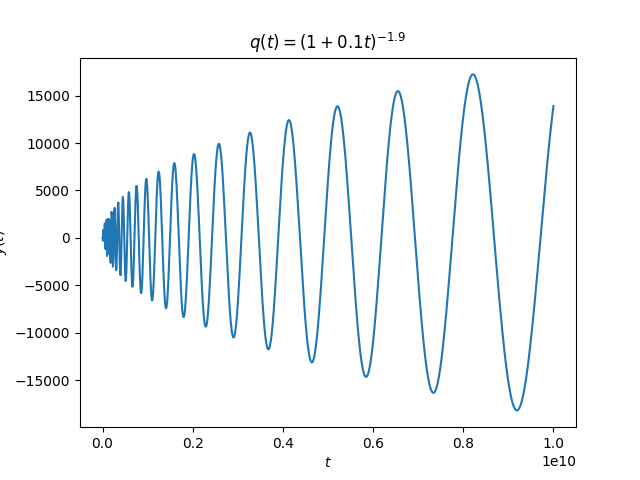
The period between zero crossings is increasing, but according to Kneser’s theorem the crossings will never stop.

Next we redo our calculation with q(t) = (1 + 0.1 t)^-2.1. Now we’re on the other side of Kneser’s theorem and so we expect oscillations to eventually stop.

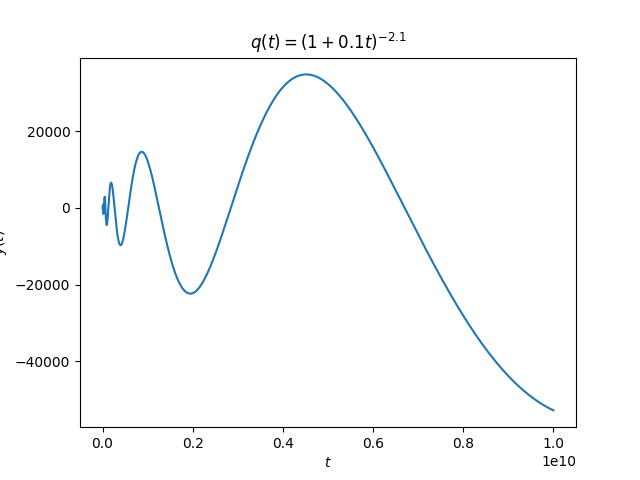
There are a lot more zero crossings than are evident in the plot; they just can’t be seen because the horizontal scale is so large.

According to Kneser’s theorem there is a last time the solution crosses zero, and I believe it occurs around 2×10²⁶.

Slowing oscillations

Example

More differential equation posts

One thought on “Slowing oscillations”