The previous post looked at ways of associating a product of four things. This post will look at associating more things, and visualizing the associations.
The number of ways to associate a product of n+1 things is the nth Catalan number, defined by
The previous post looked at products of 4 things, and there are 5 ways to do that because C3 = 5.
If we look at products of 5 things, there are 14 possibilities because C4 = 14.
In the 1950s Dov Tamari had the idea of visualizing the way associations are related. Jim Stasheff independently came up with the idea in the 1960s.
Imagine parenthesized products as vertices of a polyhedron, and connect two vertices with an edge if you can get from one to the other by one application of the associative law. The product of n terms corresponds to a polyhedron in n-2 dimensions. Such a polyhedron is called an associahedron.
If we were to do this with 4 items, we’d get a pentagon in the plane. This associahedron comes up as the commutative diagram describing the pentagon identity for monoidal categories.
If we do this with 5 items, we get a polygon in 3D. It has 14 vertices, because C4 = 14. It also has 21 edges and 9 faces.
(Quick check: V − E + F = 14 − 21 + 9 = 2. Thanks, Euler.)
I recently learned about Excalidraw, and so I drew an associahedron with Excalidraw to try it out. Here’s what I got:
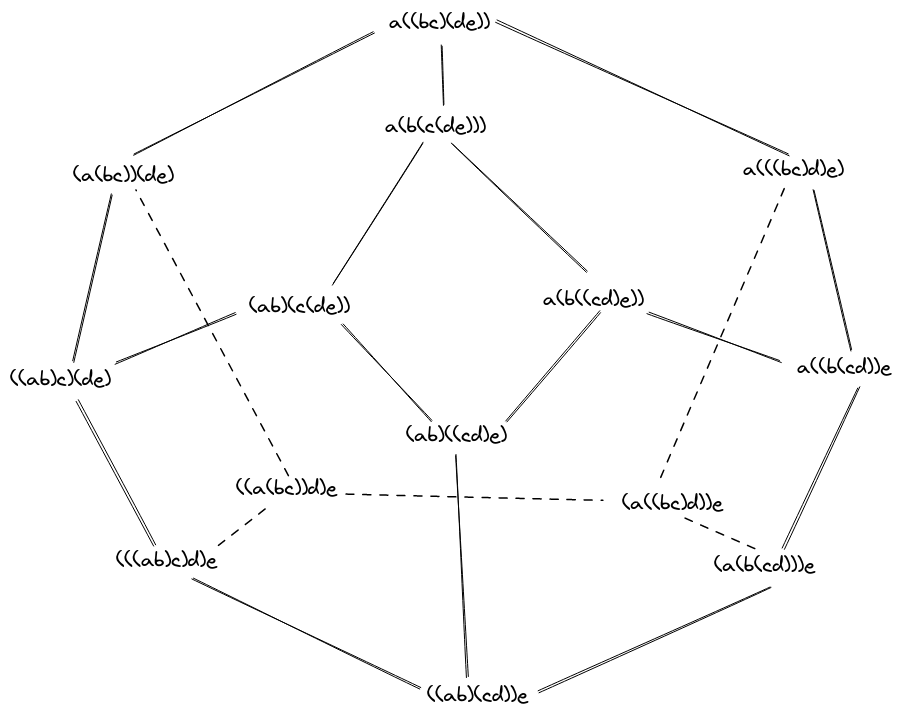
The dashed lines are edges you couldn’t see if the polyhedron were made of opaque material, but that you would see if it were transparent.
It’s not a regular solid because three faces have 4 sides and six faces have 5 sides.
Excalidraw is easy to use. It has more features than are apparent at first, which is good: you’re not immediately overwhelmed with options when you open it up, and yet when you need something you may be able to find it. For example, it’s obvious how to draw straight lines, which is probably what you want to do most of the time. But you can draw smooth curves if you need to.
