Series for arccos (inverse cosine) near 1

Suppose you need to estimate the inverse cosine of an argument near 1. There’s a series for that:

$\arccos(z) = \sqrt{2} \sqrt{1-z} \left( 1 + \frac{1-z}{12} + \frac{3}{160}(1-z)^3 + \cdots \right)$

You can find this series, for example, here.

This comes in handy, for example, when working with the analog of the Pythagorean theorem on a sphere.

You could just use the series and be on your way. But there’s a lot more going on than immediately meets the eye.

Why this shouldn’t be possible

We’re looking at a series for inverse cosine centered at 1, and yet inverse cosine is multivalued in a neighborhood of 1: for an argument slightly less than 1, there are two possible angles that have such a cosine. That matters because in order to have a power series at a point, a function has to be well behaved in a disk around that point in the complex plane. Not only is our function not well behaved, it’s not even well defined until we consider branch cuts. Also, the function arccos(z) isn’t differentiable at 1; the derivative has a singularity at 1.

In a nutshell, we’re trying to expand a function in a series at a point where the function is badly behaved. That sounds impossible, or at least ill-advised.

Why this may be possible

The series above is not a series for arccos per se. If we divide both sides of the series by √(2-2z) we see that we actually have a series for

$\frac{\arccos(z)}{\sqrt{2-2z}}$

Although arccos is badly behaved at 1, so is √(2-2z), and their ratio is well behaved at 1. In fact, it’s an analytic function and so it has a power series.

Inverse cosine has a series expansion but it does not have a power series. The series at the top is not a power series because it does not consist solely of powers of z. There’s a square root function on the right side as well, and this function is crucial to making things work.

Motivation

Why would anyone think to find a series this way, i.e. why divide by √(2-2z)?

For small values of z,

$\cos(z) \approx 1 - \frac{z^2}{2}$

and so

$\arccos(z) \approx \sqrt{2 - 2z}$

One might hope, correctly it turns out, that by dividing arccos(z) by a good approximation might yield a function nice enough to expand in a power series.

Why it is possible

Let’s plot

$\frac{\arccos(z)}{\sqrt{2-2z}}$

to see whether it looks like a reasonable function. There’s usually no middle ground in complex variables: functions are either analytic or badly behaved. Both the numerator and denominator have branch cuts, but hopefully the cuts coincide and the ratio can be extended smoothly across the cuts.

The plot below suggests that is the case.

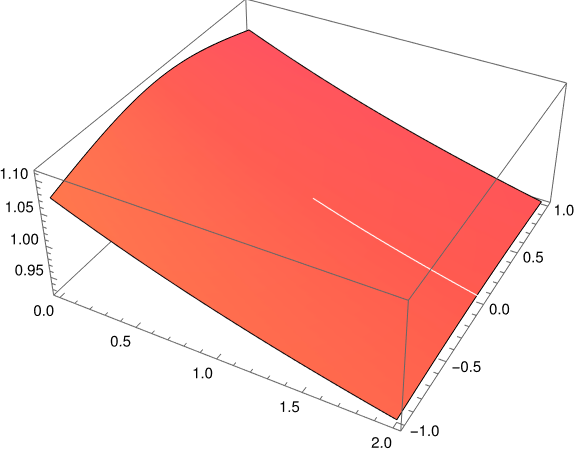
This plot was produced with

    f[z_] := ArcCos[z] / Sqrt[2 - 2 z]
    ComplexPlot3D[f[z], {z, 0 - I, 2 + I}]

The white streak across the plot is not an accidental artifact of plotting but illustrates something important.

It is not possible to extend arccos(z) to a function that is analytic for all z. You have to exclude some values of z from the domain, i.e. you have to make branch cuts, and Mathematica makes these cuts along the real axis for z ≤ -1 and z ≥ 1.

The square root function also requires a branch cut, and Mathematica chooses that branch cut to be along the negative real axis, with means we have to exclude z ≥ 1. So the branch cuts of our numerator and denominator do coincide. (Inverse cosine has an additional branch cut, but it’s not near 1 so it doesn’t matter for our purposes.)

In summary, the series at the top of the post expands arccos at a point where the function is badly behaved, by dividing it by another function that is badly defined in the same way, making a function that is well behaved.

Series for inverse cosine at 1

Why this shouldn’t be possible

Why this may be possible

Motivation

Why it is possible

Related posts

One thought on “Series for inverse cosine at 1”