Suppose you drive a distance a, turn right, then drive a distance b. How far are you from where you started?
If a and b are relatively small, then the answer is given by the Pythagorean theorem. Small here means small relative to the radius of the Earth. Any distance you drive is small enough: it matters more that roads are not perfectly straight than that the Earth is not perfectly flat.
Now suppose you fly a distance a, turn right, then fly a distance b. Now how far are you from where you started? Now the curvature of the earth might matter a good deal, and the Pythagorean theorem could give you a poor answer.
Spherical version of the Pythagorean theorem
If a and b are moderately large, we need to look at spherical triangles, not plane triangles. A “straight” line on a sphere is a piece of a great circle, a circle whose center is the center of the sphere. A spherical triangle has three straight sides, straight in the sense of a straight line on a sphere. We need to consider a spherical triangle with sides a and b that meet at right angles, and we want to find the length of the hypotenuse c of the spherical triangle.
The spherical analog of the Pythagorean theorem says
cos(c) = cos(a) cos(b).
This looks weird the first time you see it, because you’re taking the cosine of a side rather than an angle. But on a sphere, the sides are angles. For example, if a side of the triangle is on a meridian, we could measure its length in degrees of latitude. But the theorem above does not require sides to be lined up with any coordinate system. It only requires that the sides a and b meet at a right angle.
Small spherical triangles
Let’s suppose for a moment that a and b are small when measured in radians, small enough that a², b², and ab are negligible compared to a and b. Then we can use the approximation
cos(x) ≈ 1 − x²/2
in the theorem above to show that
c² ≈ a² + b².
This is reassuring since we know the Pythagorean theorem holds for human-scale distances on our planet.
Example with a big triangle
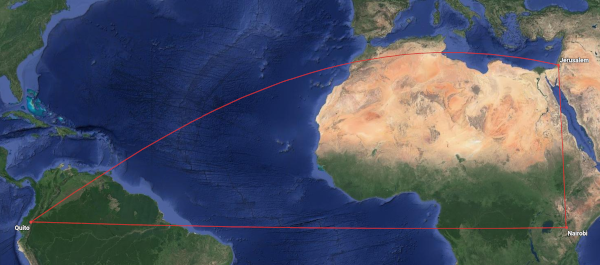
Now let’s look at a big triangle. The vertices have longitude and latitude (−80°, 0°), (35°, 0°), and (35°, 30°). These correspond approximately to Quito, Nairobi, and Jerusalem. So a = 115° and b = 30°. We can solve for c and find it equals 111°.
A minute of latitude is a nautical mile; the nautical mile is defined the way to make these kinds of calculations easier. A nautical mile is about 15% longer than a mile.
A degree of a great circle is 60 nautical miles. So our hypotenuse of 111 degrees is 6,660 nautical miles. If we had used the Pythagorean theorem, we would have overestimated this distance as 7,130 nautical miles.
Notice that the triangle with vertices at Quito, Nairobi, and Jerusalem doesn’t look like a triangle when projected flat. Two legs look straight because they follow lines of constant latitude or longitude. But the flight from Jerusalem to Quito is just as straight as the other flights if you look at it on a globe.
Not so great circles
In the example above, I chose Quito and Nairobi because they were near the equator. The equator is a great circle.
Suppose I’d chosen Houston and Wuhan instead. Both cities are at about 30° latitude. I could not find the distance between the two cities by simply subtracting their longitudes because the 30th parallel is not a great circle. Spherical geometry is generally more involved than in the example above.
A great circle path from Houston to Wuhan would not follow the 30th parallel but would actually cross Alaska. The great circle distance is 6,800 nautical miles. Flying along a path of 30° latitude would add an extra 1,000 nautical miles to the flight.

Can you suggest an introductory text on spherical geometry please John?
There’s a book that came out a few years ago: Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry by Glen Van Brummelen.
It’s a mixture of history and mathematics. If your primary goal is to learn the math, read the first four chapters lightly, but concentrate on chapters 5 and 6.