Take an arbitrary triangle and draw the trisectors of each angle. Morley’s theorem says that the trisector lines will intersect at the vertices of an equilateral triangle.
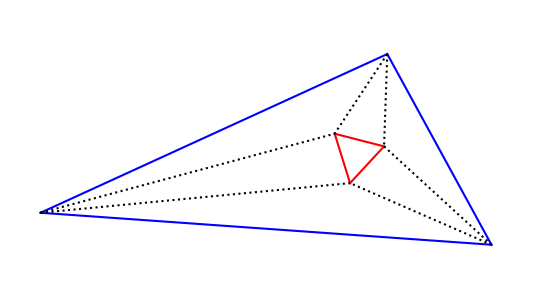
This theorem is surprising because out of a triangle with no symmetry pops a triangle with three-fold symmetry.
The theorem is also historically surprising. It’s a theorem of Euclidean geometry discovered around 1900, twenty three centuries after Euclid. You might reasonably suppose that Euclidean geometry had been thoroughly picked over by 1900, and yet Morley found something nobody else had noticed.
Update: See the next post for Napoleon’s theorem, another theorem where an equilateral triangle is associated with a general triangle.

Perhaps no-one pursued ramifications of trisections for a long time because trisections are hard to construct?