Napoleon’s theorem is usually presented as I presented it in the previous post.
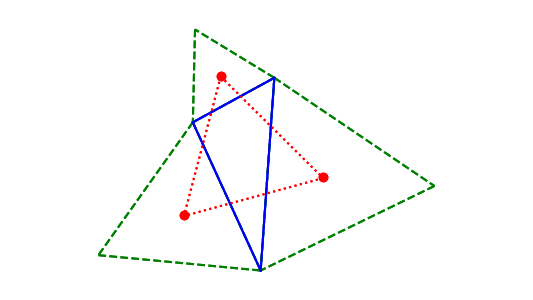
You start with a triangle (solid blue) and add equilateral triangles (dashed green) on the outside of the triangle. When you connect the centroids of these triangles you get a (dotted red) equilateral triangle.
But Napoleon’s theorem is more general than this. It says you could also add the triangles to the inside. The result is much harder to parse visually. The following diagram flips each green triangle over.
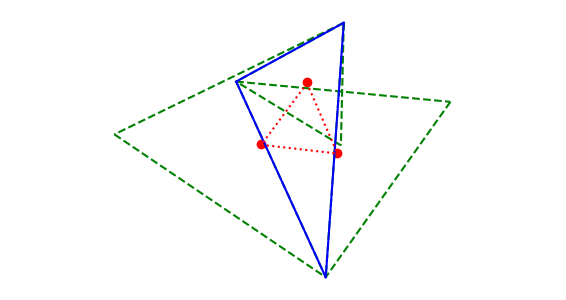
You still get an equilateral triangle when you connect the centroids, but it’s a different triangle.

Can rhis be generalized to isosceles triangles with the same top angle? If so, which of the three centers?
what happens in between … interpolating from outside to inside? might have to try geogebra to viz this …