Euler sine product convergence visualized

Euler’s product formula for sine is

$\sin(x) = x \prod_{n=1}^\infty \left(1 - \frac{x^2}{\pi^2n^2}\right)$

To visualize the convergence of the infinite product, let’s look at the error in approximating sin(πx) with the Nth partial product of the infinite product, i.e.

$\sin(\pi x) - \pi x \prod_{n=1}^N \left(1 - \frac{x^2}{n^2}\right)$

Here’s a plot of the partial products.

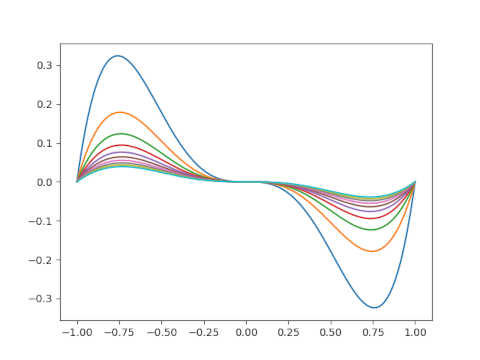
We knew before making the plot that the error had to go to zero as N increases; otherwise Euler’s product wouldn’t converge. But it’s interesting to visualize how the error goes to zero.