Taylor polynomials are terrific local approximations but poor global approximations. Taylor polynomials are optimal in some sense near their center, but are seldom the best choice over a large interval.
This post will look at approximating sin(πx) over [−1, 1] with fifth degree polynomials.
First, this plot compares the approximation error for a fifth order polynomials based on Taylor series and a fifth order polynomial based on Euler’s series from the previous post.
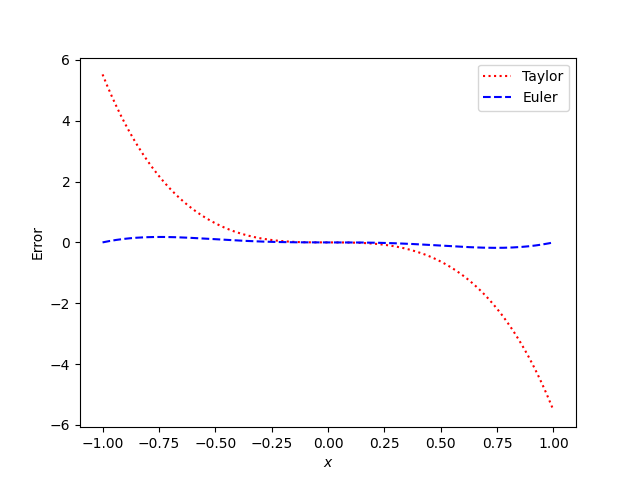
Very near 0 the Taylor approximation is more accurate, but over an entire period of sine, the polynomial based on Euler’s series is much better.
But we can do even better by using a fifth order polynomial based on the first few terms of a Chebyshev series to approximate sine.
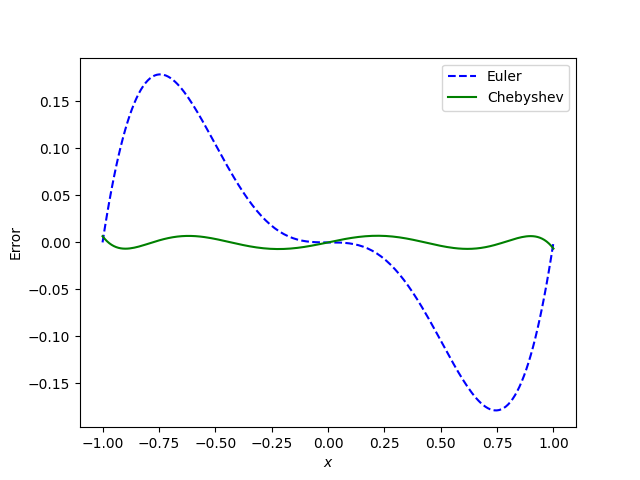
Chebyshev series may not have minimal sup-norm error, but there is a theorem that says they are never far from optimal. See the bottom of this post.
