Hyperbolic secant distribution

Posted on by John

I hadn’t run into the hyperbolic secant distribution until I saw a paper by Peng Ding [1] recently. If C is a standard Cauchy random variable, then (2/π) log |C| has a hyperbolic secant distribution. Three applications of this distribution are given in [1].

Ding’s paper contains a plot comparing the density functions for the hyperbolic secant distribution, the standard normal distribution, and the logistic distribution with scale √3/π. The scale for the logistic was chosen so that all three distributions would have variance 1.

There’s something interesting about comparing logistic distribution and the hyperbolic secant distribution densities: the former is the square of the latter, aside from some scaling, and yet the two functions are similar. You don’t often approximate a function by its square.

Here’s a plot of the two densities.

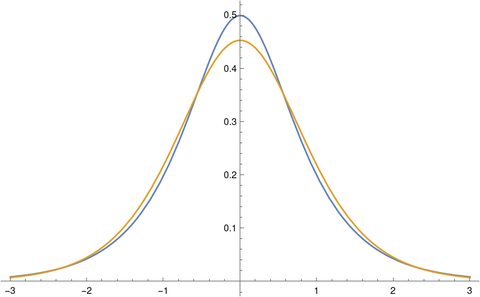
The hyperbolic secant density, the blue curve, crosses the logistic density around ± 0.56 and around ± 2.33.

The hyperbolic secant distribution has density

f_H(x) = \frac{1}{2} \text{sech} \left(\frac{\pi x}{2} \right)

and the logistic distribution, as scaled in above, has density

f_L(x) = \frac{\pi}{4\sqrt 3} \,\text{sech}^2 \left(\frac{\pi x}{2\sqrt 3} \right)

and so

\frac{\pi}{\sqrt 3} \,f_H(x)^2 = f_L(x)

Related posts

[1] Peng Ding. Three Occurrences of the Hyperbolic-Secant Distribution. The American Statistician , Feb 2014, Vol. 68, No. 1 (2014), pp. 32-35