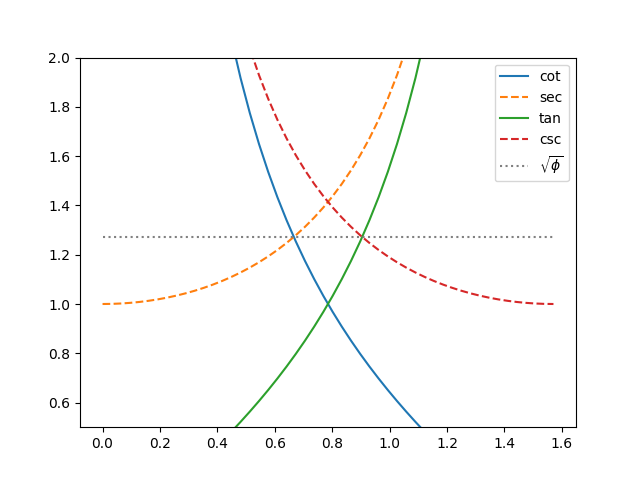
Here’s a curious fact. The graphs of cotangent and secant cross at the same height as the graphs of tangent and cosecant, and this common height is the square root of the golden ratio φ.
It’s also the case that the graphs of hyperbolic cosecant and hyperbolic cosine, and the graphs of hyperbolic sine and hyperbolic cotangent, also cross at the same height, √φ.
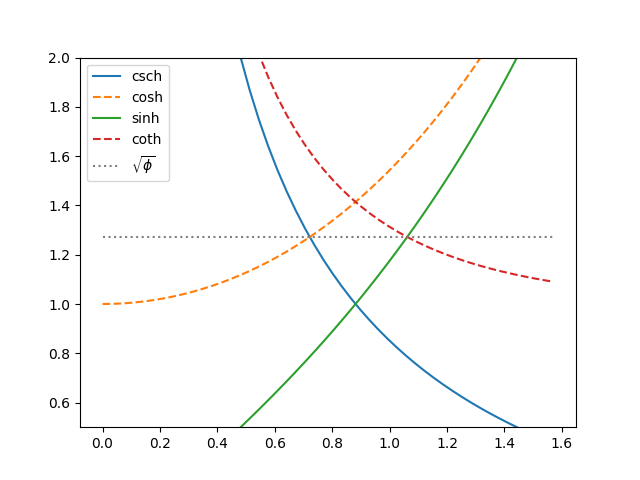
Source: P. J. Leah and J. B. Wilker. Hyperbolic and Trigonometric Crossing Points. Mathematics Magazine, Vol. 63, No. 3 (Jun., 1990), pp. 179-183

That is an interesting result. A little geometric identity work and some algebra lead to it, but it is very interesting that it comes out like that. Once you set up the equation for where the functions cross you end up with a quadratic that is similar to the quadratic relationship that defines the golden ratio. At that point I knew where it was heading, but had to clear a lot of radicals to get to the final answer.
Out of curiosity, I also calculated the kite-like area enclosed by the 4 concerned trigonometric functions.
I calculated concerned area S as :
S = ln(1/Phi*(10-6*Phi)/(3-2*sqrt(2)), approx. ~ 0.049835
As expected, this result also contains the constant Phi.
(Phi = golden ratio : 1.618033…)